广东省梅州市五华县2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-10-16 类型:期末考试
一、单选题
-
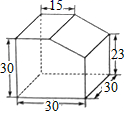
1. 如图所示的几何体,它的左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 一元二次方程x2﹣2x+3=0的一次项和常数项分别是( )A、2和3 B、﹣2和3 C、﹣2x和3 D、2x和33. 若反比例函数y= (k≠0)的图象经过(2,3),则k的值为( )A、5 B、﹣5 C、6 D、﹣64. 四条线段a,b,c,d成比例,其中b=3cm,c=8cm,d=12cm,则a=( )A、2cm B、4cm C、6cm D、8cm5. 下列判断错误的是( )A、有两组邻边相等的四边形是菱形 B、有一角为直角的平行四边形是矩形 C、对角线互相垂直且相等的平行四边形是正方形 D、矩形的对角线互相平分且相等6. 关于 的方程 的根的情况,正确的是( ).A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根7. 在平面直角坐标系中,以原点O为位似中心,把△ABC放大得到△A1B1C1 , 使它们的相似比为1:2,若点A的坐标为(2,2),则它的对应点A1的坐标一定是( )A、(﹣2,﹣2) B、(1,1) C、(4,4) D、(4,4)或(﹣4,﹣4)8. 如图,EF过矩形ABCD对角线的交点O,且分别交AB,CD于E,F,矩形ABCD内的一个动点P落在阴影部分的概率是( )
2. 一元二次方程x2﹣2x+3=0的一次项和常数项分别是( )A、2和3 B、﹣2和3 C、﹣2x和3 D、2x和33. 若反比例函数y= (k≠0)的图象经过(2,3),则k的值为( )A、5 B、﹣5 C、6 D、﹣64. 四条线段a,b,c,d成比例,其中b=3cm,c=8cm,d=12cm,则a=( )A、2cm B、4cm C、6cm D、8cm5. 下列判断错误的是( )A、有两组邻边相等的四边形是菱形 B、有一角为直角的平行四边形是矩形 C、对角线互相垂直且相等的平行四边形是正方形 D、矩形的对角线互相平分且相等6. 关于 的方程 的根的情况,正确的是( ).A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根7. 在平面直角坐标系中,以原点O为位似中心,把△ABC放大得到△A1B1C1 , 使它们的相似比为1:2,若点A的坐标为(2,2),则它的对应点A1的坐标一定是( )A、(﹣2,﹣2) B、(1,1) C、(4,4) D、(4,4)或(﹣4,﹣4)8. 如图,EF过矩形ABCD对角线的交点O,且分别交AB,CD于E,F,矩形ABCD内的一个动点P落在阴影部分的概率是( )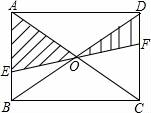 A、 B、 C、 D、9. 如图,在矩形ABCD中,点M从点B出发沿BC向点C运动,点E、F别是AM、MC的中点,则EF的长随着M点的运动( )
A、 B、 C、 D、9. 如图,在矩形ABCD中,点M从点B出发沿BC向点C运动,点E、F别是AM、MC的中点,则EF的长随着M点的运动( )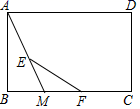 A、不变 B、变长 C、变短 D、先变短再变长10. 如图,边长为1的正方形ABCD中,点E在CB的延长线上,连接ED交AB于点F,AF=x(0.2≤x≤0.8),EC=y.则在下面函数图象中,大致能反映y与x之间函数关系的是( )
A、不变 B、变长 C、变短 D、先变短再变长10. 如图,边长为1的正方形ABCD中,点E在CB的延长线上,连接ED交AB于点F,AF=x(0.2≤x≤0.8),EC=y.则在下面函数图象中,大致能反映y与x之间函数关系的是( )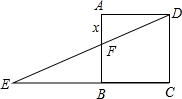 A、
A、 B、
B、 C、
C、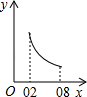 D、
D、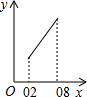
二、填空题
-
11. 若两个相似三角形的面积比为1∶4,则这两个相似三角形的周长比是 .12. 若函数y= 的图象在每个象限内y的值随x值的增大而增大,则m的取值范围为 .13. 已知 (x、y、z均不为零),则 .14. 已知点P是线段AB的黄金分割点,AP>PB.若AB=10.则AP=(结果保留根号).15. 若 是方程 的两个根,则 的值为16. 如图,点P在函数y= 的图象上,PA⊥x轴于点A , PB⊥y轴于点B , 且△APB的面积为4,则k等于 .
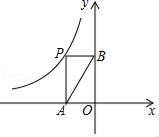 17. 如图,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.过点D作DG∥BE,交BC于点G,连接FG交BD于点O.若AB=6,AD=8,则DG的长为 .
17. 如图,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.过点D作DG∥BE,交BC于点G,连接FG交BD于点O.若AB=6,AD=8,则DG的长为 .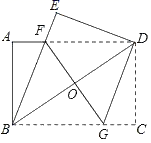
三、解答题
-
18. 解方程:(x+2)(x-5)=18.19. 已知线段AC
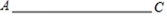 (1)、尺规作图:作菱形ABCD,使AC是菱形的一条对角线(保留作图痕迹,不要求写作法);(2)、若AC=8,BD=6,求菱形的边长.20. 如图,△ABC中,AC=BC,CD⊥AB于点D,四边形DBCE是平行四边形.
(1)、尺规作图:作菱形ABCD,使AC是菱形的一条对角线(保留作图痕迹,不要求写作法);(2)、若AC=8,BD=6,求菱形的边长.20. 如图,△ABC中,AC=BC,CD⊥AB于点D,四边形DBCE是平行四边形.求证:四边形ADCE是矩形.
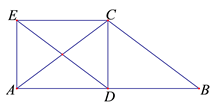 21. 粤东农批﹒2019球王故里五华马拉松赛于12月1日在广东五华举行,组委会为了做好运动员的保障工作,沿途设置了4个补给站,分别是:A(粤东农批)、B(奥体中心)、C(球王故里)和D(滨江中路),志愿者小明和小红都计划各自在这4个补给站中任意选择一个进行补给服务,每个补给站被选择的可能性相同.(1)、小明选择补给站C(球王故里)的概率是多少?(2)、用树状图或列表的方法,求小明和小红恰好选择同一个补给站的概率.22. 2018年非洲猪瘟疫情暴发后,2019年猪肉价格不断走高,引起了民众与政府的高度关注,据统计:2019年12月份猪肉价格比2019年年初上涨了30%,某市民2019年12月3日在某超市购买1千克猪肉花了52元.(1)、问:2019年年初猪肉的价格为每千克多少元?(2)、某超市将进货价为每千克39元的猪肉,按2019年12月3日价格出售,平均一天能销售出100千克,经调查表明:猪肉的售价每千克下降1元,其日销售量就增加10千克,超市为了实现销售猪肉每天有1320元的利润,并且尽可能让顾客得到实惠,猪肉的售价应该下降多少元?23. 已知,如图,在平行四边形ABCD中,M是BC边的中点,E是边BA延长线上的一点,连接EM,分别交线段AD于点F、AC于点G.
21. 粤东农批﹒2019球王故里五华马拉松赛于12月1日在广东五华举行,组委会为了做好运动员的保障工作,沿途设置了4个补给站,分别是:A(粤东农批)、B(奥体中心)、C(球王故里)和D(滨江中路),志愿者小明和小红都计划各自在这4个补给站中任意选择一个进行补给服务,每个补给站被选择的可能性相同.(1)、小明选择补给站C(球王故里)的概率是多少?(2)、用树状图或列表的方法,求小明和小红恰好选择同一个补给站的概率.22. 2018年非洲猪瘟疫情暴发后,2019年猪肉价格不断走高,引起了民众与政府的高度关注,据统计:2019年12月份猪肉价格比2019年年初上涨了30%,某市民2019年12月3日在某超市购买1千克猪肉花了52元.(1)、问:2019年年初猪肉的价格为每千克多少元?(2)、某超市将进货价为每千克39元的猪肉,按2019年12月3日价格出售,平均一天能销售出100千克,经调查表明:猪肉的售价每千克下降1元,其日销售量就增加10千克,超市为了实现销售猪肉每天有1320元的利润,并且尽可能让顾客得到实惠,猪肉的售价应该下降多少元?23. 已知,如图,在平行四边形ABCD中,M是BC边的中点,E是边BA延长线上的一点,连接EM,分别交线段AD于点F、AC于点G. (1)、证明: ∽(2)、求证: ;24. 如图,一次函数y1=mx+n与反比例函数y2= (x>0)的图象分别交于点A(a,4)和点B(8,1),与坐标轴分别交于点C和点D.
(1)、证明: ∽(2)、求证: ;24. 如图,一次函数y1=mx+n与反比例函数y2= (x>0)的图象分别交于点A(a,4)和点B(8,1),与坐标轴分别交于点C和点D.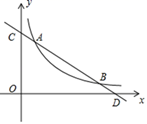 (1)、求一次函数与反比例函数的解析式;(2)、观察图象,当x>0时,直接写出y1>y2的解集;(3)、若点P是x轴上一动点,当△COD与△ADP相似时,求点P的坐标.25. 在矩形ABCD中,AB=3,BC=4,E,F是对角线AC上的两个动点,分别从A,C同时出发相向而行,速度均为1cm/s,运动时间为t秒,0≤t≤5.
(1)、求一次函数与反比例函数的解析式;(2)、观察图象,当x>0时,直接写出y1>y2的解集;(3)、若点P是x轴上一动点,当△COD与△ADP相似时,求点P的坐标.25. 在矩形ABCD中,AB=3,BC=4,E,F是对角线AC上的两个动点,分别从A,C同时出发相向而行,速度均为1cm/s,运动时间为t秒,0≤t≤5. (1)、AE= , EF=(2)、若G,H分别是AB,DC中点,求证:四边形EGFH是平行四边形.( 相遇时除外)(3)、在(2)条件下,当t为何值时,四边形EGFH为矩形.
(1)、AE= , EF=(2)、若G,H分别是AB,DC中点,求证:四边形EGFH是平行四边形.( 相遇时除外)(3)、在(2)条件下,当t为何值时,四边形EGFH为矩形.