广东省梅州市2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-10-16 类型:期末考试
一、单选题
-
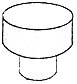
1. 如图所示的工件,其俯视图是( )
 A、
A、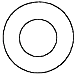 B、
B、 C、
C、 D、
D、 2. 方程x2=3x的解为( )A、x=3 B、x=0 C、x1=0,x2=﹣3 D、x1=0,x2=33. 已知反比例函数y= 的图象经过点(3,2),那么下列四个点中,也在这个函数图象上的是( )
2. 方程x2=3x的解为( )A、x=3 B、x=0 C、x1=0,x2=﹣3 D、x1=0,x2=33. 已知反比例函数y= 的图象经过点(3,2),那么下列四个点中,也在这个函数图象上的是( )
A、(3,-2) B、(-2,-3) C、(1,-6) D、(-6,1)4. 一个不透明的袋中装有2个红球和4个黄球,这些球除颜色外完全相同.从袋中随机摸出一个球,摸到黄球的概率是( )A、 B、 C、 D、5. 如图,在△ABC中,DE∥BC,DE分别与AB、AC相交于点D、E,若AD=4,DB=2,则EC:AE的值为( )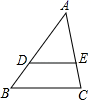 A、 B、 C、 D、6. 若 是方程 的两根,则 的值是( )A、8 B、-8 C、-6 D、67. 如图,点 、 分别在 的边 、 上,且 与 不平行.下列条件中,能判定 与 相似的是( )
A、 B、 C、 D、6. 若 是方程 的两根,则 的值是( )A、8 B、-8 C、-6 D、67. 如图,点 、 分别在 的边 、 上,且 与 不平行.下列条件中,能判定 与 相似的是( )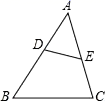 A、 B、 C、 D、8. 某企业2018年初获利润300万元,到2020年初计划利润达到507万元.设这两年的年利润平均增长率为x.应列方程是( )A、300(1+x)=507 B、300(1+x)2=507 C、300(1+x)+300(1+x)2=507 D、300+300(1+x)+300(1+x)2=5079. 如图,点O是矩形ABCD的对角线AC的中点, 交AD于点M,若 , ,则OB的长为
A、 B、 C、 D、8. 某企业2018年初获利润300万元,到2020年初计划利润达到507万元.设这两年的年利润平均增长率为x.应列方程是( )A、300(1+x)=507 B、300(1+x)2=507 C、300(1+x)+300(1+x)2=507 D、300+300(1+x)+300(1+x)2=5079. 如图,点O是矩形ABCD的对角线AC的中点, 交AD于点M,若 , ,则OB的长为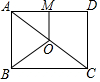 A、4 B、5 C、6 D、10. 函数y=ax2+a与 (a≠0),在同一坐标系中的图象可能是( )A、
A、4 B、5 C、6 D、10. 函数y=ax2+a与 (a≠0),在同一坐标系中的图象可能是( )A、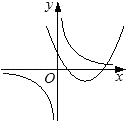 B、
B、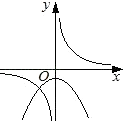 C、
C、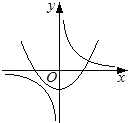 D、
D、
二、填空题
-
11. 已知 ,则 =12. 小明同学身高1.5米,经太阳光照射,在地面的影长为2米,他此时测得旗杆在同一地面的影长为12米,那么旗杆高为米.13. 点A(﹣5,y1),B(3,y2)都在双曲线y= ,则y1 , y2的大小关系是 .14. 若△ABC∽△A′B′C′,相似比为1:3,则△ABC与△A′B′C′的面积之比为 .15. 如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落在M处,∠BEF=70°,则∠ABE=度.
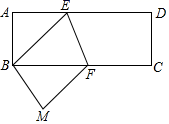 16. 如图,在菱形ABCD中,E是BC边上的点,AE交BD于点F,若EC=2BE,则 的值是 .
16. 如图,在菱形ABCD中,E是BC边上的点,AE交BD于点F,若EC=2BE,则 的值是 .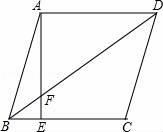 17. 如图,在菱形ABCD中,边长为1,∠A=60˚,顺次连接菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去,…,则四边形A2019B2019C2019D2019的面积是.
17. 如图,在菱形ABCD中,边长为1,∠A=60˚,顺次连接菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去,…,则四边形A2019B2019C2019D2019的面积是.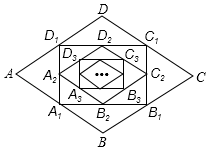
三、解答题
-
18. 解一元二次方程:x2﹣5x+6=0.19. 如图,已知△ABC.
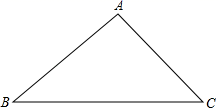 (1)、尺规作图,画出线段AB的垂直平分线(不写作法,保留作图痕迹);(2)、设AB的垂直平分线与BA交于点D,与BC交于点E,连结AE.若∠B=40°,求∠BEA的度数.20. 小明、小亮两人用如图所示的两个分隔均匀的转盘做游戏:分别转动两个转盘,转盘停止后,将两个指针所指数字相加(若指针恰好停在分割线上,则重转一次).如果这两个数字之和小于8(不包括8),则小明获胜;否则小亮获胜。
(1)、尺规作图,画出线段AB的垂直平分线(不写作法,保留作图痕迹);(2)、设AB的垂直平分线与BA交于点D,与BC交于点E,连结AE.若∠B=40°,求∠BEA的度数.20. 小明、小亮两人用如图所示的两个分隔均匀的转盘做游戏:分别转动两个转盘,转盘停止后,将两个指针所指数字相加(若指针恰好停在分割线上,则重转一次).如果这两个数字之和小于8(不包括8),则小明获胜;否则小亮获胜。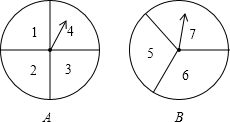 (1)、利用列表法或画树状图的方法表示游戏所有可能出现的结果;(2)、这个游戏对双方公平吗?请说明理由.21. 已知一元二次方程x2﹣3x+m=0.(1)、若方程有两个不相等的实数根,求m的取值范围.(2)、若方程有两个相等的实数根,求此时方程的根.22. 某中学课外兴趣活动小组准备围建一个矩形苗圃,其中一边靠墙,另外三边用长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃垂直于墙的一边长为x米.
(1)、利用列表法或画树状图的方法表示游戏所有可能出现的结果;(2)、这个游戏对双方公平吗?请说明理由.21. 已知一元二次方程x2﹣3x+m=0.(1)、若方程有两个不相等的实数根,求m的取值范围.(2)、若方程有两个相等的实数根,求此时方程的根.22. 某中学课外兴趣活动小组准备围建一个矩形苗圃,其中一边靠墙,另外三边用长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃垂直于墙的一边长为x米.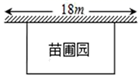 (1)、若苗圃的面积为72平方米,求x的值;(2)、这个苗圃的面积能否是120平方米?请说明理由.23. 如图,在平行四边形ABCD中,点E , F , G , H分别在边AB , BC , CD , DA上,AE=CG , AH=CF , 且EG平分∠HEF .
(1)、若苗圃的面积为72平方米,求x的值;(2)、这个苗圃的面积能否是120平方米?请说明理由.23. 如图,在平行四边形ABCD中,点E , F , G , H分别在边AB , BC , CD , DA上,AE=CG , AH=CF , 且EG平分∠HEF .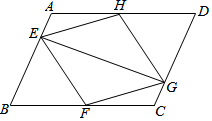 (1)、求证:△AEH≌△CGF .(2)、若∠EFG=90°.求证:四边形EFGH是正方形.24. 如图,一次函数y=x+4的图象与反比例函数y= (k为常数且k≠0)的图象交于A(﹣1,3),B(b,1)两点.
(1)、求证:△AEH≌△CGF .(2)、若∠EFG=90°.求证:四边形EFGH是正方形.24. 如图,一次函数y=x+4的图象与反比例函数y= (k为常数且k≠0)的图象交于A(﹣1,3),B(b,1)两点.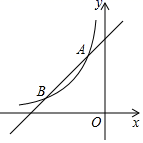 (1)、求反比例函数的表达式;(2)、在x轴上找一点P,使PA+PB的值最小,并求满足条件的点P的坐标;(3)、连接OA,OB,求△OAB的面积.25. 如图,在四边形ABCD中,AB∥DC,BC>AD,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5).
(1)、求反比例函数的表达式;(2)、在x轴上找一点P,使PA+PB的值最小,并求满足条件的点P的坐标;(3)、连接OA,OB,求△OAB的面积.25. 如图,在四边形ABCD中,AB∥DC,BC>AD,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5).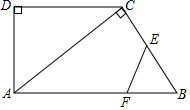 (1)、求证:△ACD∽△BAC;(2)、求DC的长;(3)、试探究:△BEF可以为等腰三角形吗?若能,求t的值;若不能,请说明理由.
(1)、求证:△ACD∽△BAC;(2)、求DC的长;(3)、试探究:△BEF可以为等腰三角形吗?若能,求t的值;若不能,请说明理由.