广东省揭阳市普宁市2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-10-16 类型:期末考试
一、单选题
-
1. 如图所示几何体的俯视图是( )
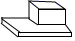 A、
A、 B、
B、 C、
C、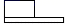 D、
D、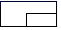 2. 下列说法中错误的是( )A、四边相等的四边形是菱形 B、对角线垂直的平行四边形是菱形 C、菱形的对角线互相垂直且相等 D、菱形的邻边相等3. 已知 ,下列变形错误的是( )
2. 下列说法中错误的是( )A、四边相等的四边形是菱形 B、对角线垂直的平行四边形是菱形 C、菱形的对角线互相垂直且相等 D、菱形的邻边相等3. 已知 ,下列变形错误的是( )
A、 B、 C、 D、4. 已知关于 的一元二次方程 有两个相等的实数根,则 ( )A、4 B、2 C、1 D、﹣45. 若点 , , 在反比例函数 的图象上,则y1 , y2 , y3的大小关系是( )A、 B、 C、 D、6. 抛物线y=x2+2x+m﹣1与x轴有两个不同的交点,则m的取值范围是( )A、m<2 B、m>2 C、0<m≤2 D、m<﹣27.如图,下列条件不能判定△ADB∽△ABC的是( )
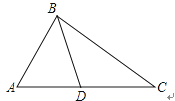 A、∠ABD=∠ACB B、∠ADB=∠ABC C、AB2=AD•AC D、8. 关于抛物线 ,下列结论中正确的是( )A、对称轴为直线 B、当 时, 随 的增大而减小 C、与 轴没有交点 D、与 轴交于点9. 如图,点A在反比例函数y= (x>0)的图象上,过点A作AB⊥x轴,垂足为点B,点C在y轴上,则△ABC的面积为( )
A、∠ABD=∠ACB B、∠ADB=∠ABC C、AB2=AD•AC D、8. 关于抛物线 ,下列结论中正确的是( )A、对称轴为直线 B、当 时, 随 的增大而减小 C、与 轴没有交点 D、与 轴交于点9. 如图,点A在反比例函数y= (x>0)的图象上,过点A作AB⊥x轴,垂足为点B,点C在y轴上,则△ABC的面积为( ) A、3 B、2 C、 D、110. 如图,在正方形 中,点 是对角线 的交点,过点 作射线分别交 于点 ,且 ,交 于点 .给出下列结论: ; C; 四边形 的面积为正方形 面积的 ; .其中正确的是( )
A、3 B、2 C、 D、110. 如图,在正方形 中,点 是对角线 的交点,过点 作射线分别交 于点 ,且 ,交 于点 .给出下列结论: ; C; 四边形 的面积为正方形 面积的 ; .其中正确的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
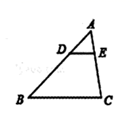
11. 计算: .12. 若一元二次方程 的两根为 , ,则 .13. 如图,在 中, , , ,则 的长为 .
 14. 在平面直角坐标系中, 与 位似,位似中心为原点 ,点 与点 是对应顶点,且点A,点 的坐标分别是 , ,那么 与 的相似比为 .15. 如图,校园内有一棵与地面垂直的树,数学兴趣小组两次测量它在地面上的影子,第一次是阳光与地面成60°角时,第二次是阳光与地面成30°角时,两次测量的影长相差8米,则树高米.(结果保留根号)
14. 在平面直角坐标系中, 与 位似,位似中心为原点 ,点 与点 是对应顶点,且点A,点 的坐标分别是 , ,那么 与 的相似比为 .15. 如图,校园内有一棵与地面垂直的树,数学兴趣小组两次测量它在地面上的影子,第一次是阳光与地面成60°角时,第二次是阳光与地面成30°角时,两次测量的影长相差8米,则树高米.(结果保留根号) 16. 某种商品每件进价为20元,调查表明:在某段时间内若以每件x元(20≤x≤30,且x为整数)出售,可卖出(30﹣x)件.若使利润最大,每件的售价应为元.
16. 某种商品每件进价为20元,调查表明:在某段时间内若以每件x元(20≤x≤30,且x为整数)出售,可卖出(30﹣x)件.若使利润最大,每件的售价应为元.
17. 如图,菱形 的边长为1, ,以对角线 为一边,在如图所示的一侧作相同形状的菱形 ,再依次作菱形 ,菱形 ,……,则菱形 的边长为 .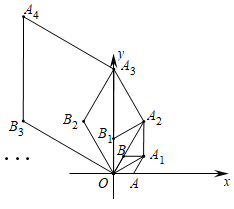
三、解答题
-
18. 解方程19. 如图,△ABC中,AD⊥BC,垂足是D,若BC=14,AD=12,tan∠BAD= ,求sinC的值.
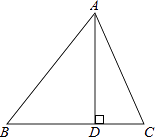 20. 已知 是 的反比例函数,下表给出了 与 的一些值.
20. 已知 是 的反比例函数,下表给出了 与 的一些值.…
-4
-2
-1
1
3
4
…
…
-2
6
3
…
 (1)、求出这个反比例函数的表达式;(2)、根据函数表达式完成上表;(3)、根据上表,在下图的平面直角坐标系中作出这个反比例函数的图象.21. 一个不透明的口袋中有4个大小、质地完全相同的乒乓球,球面上分别标有数-1,2,-3,4.(1)、摇匀后任意摸出1个球,则摸出的乒乓球球面上的数是负数的概率为.(2)、摇匀后先从中任意摸出1个球(不放回),再从余下的3个球中任意摸出1个球,用列表或画树状图的方法求两次摸出的乒乓球球面上的数之和是正数的概率.22. 随着粤港澳大湾区建设的加速推进,广东省正加速布局以5G等为代表的战略性新兴产业,据统计,目前广东5G基站的数量约1.5万座,计划到2020年底,全省5G基站数是目前的4倍,到2022年底,全省5G基站数量将达到17.34万座。(1)、计划到2020年底,全省5G基站的数量是多少万座?;(2)、按照计划,求2020年底到2022年底,全省5G基站数量的年平均增长率。23. 如图,在菱形ABCD中,对角线AC,BD相交于点O,E是CD的中点,连接OE.过点C作CF//BD交OE的延长线于点F,连接DF.
(1)、求出这个反比例函数的表达式;(2)、根据函数表达式完成上表;(3)、根据上表,在下图的平面直角坐标系中作出这个反比例函数的图象.21. 一个不透明的口袋中有4个大小、质地完全相同的乒乓球,球面上分别标有数-1,2,-3,4.(1)、摇匀后任意摸出1个球,则摸出的乒乓球球面上的数是负数的概率为.(2)、摇匀后先从中任意摸出1个球(不放回),再从余下的3个球中任意摸出1个球,用列表或画树状图的方法求两次摸出的乒乓球球面上的数之和是正数的概率.22. 随着粤港澳大湾区建设的加速推进,广东省正加速布局以5G等为代表的战略性新兴产业,据统计,目前广东5G基站的数量约1.5万座,计划到2020年底,全省5G基站数是目前的4倍,到2022年底,全省5G基站数量将达到17.34万座。(1)、计划到2020年底,全省5G基站的数量是多少万座?;(2)、按照计划,求2020年底到2022年底,全省5G基站数量的年平均增长率。23. 如图,在菱形ABCD中,对角线AC,BD相交于点O,E是CD的中点,连接OE.过点C作CF//BD交OE的延长线于点F,连接DF.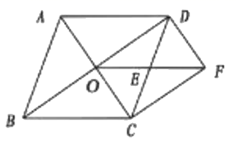
求证:
(1)、△ODE≌△FCE;(2)、四边形OCFD是矩形。24. 如图,在平面直角坐标系中,抛物线 与 轴交于 , 两点,与 轴交于点 ,直线 经过 , 两点,抛物线的顶点为 ,对称轴与 轴交于点 .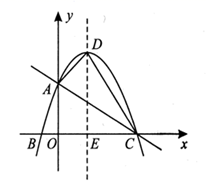 (1)、求此抛物线的解析式;(2)、求 的面积;(3)、在抛物线上是否存在一点 ,使它到 轴的距离为4,若存在,请求出点 的坐标,若不存在,则说明理由.25. 如图1,在矩形 中, , , 是 边上一点,连接 ,将矩形 沿 折叠,顶点 恰好落在 边上点 处,延长 交 的延长线于点 .
(1)、求此抛物线的解析式;(2)、求 的面积;(3)、在抛物线上是否存在一点 ,使它到 轴的距离为4,若存在,请求出点 的坐标,若不存在,则说明理由.25. 如图1,在矩形 中, , , 是 边上一点,连接 ,将矩形 沿 折叠,顶点 恰好落在 边上点 处,延长 交 的延长线于点 .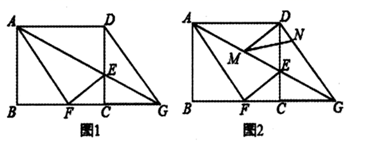 (1)、求线段 的长;(2)、如图2, , 分别是线段 , 上的动点(与端点不重合),且 .
(1)、求线段 的长;(2)、如图2, , 分别是线段 , 上的动点(与端点不重合),且 .①求证: ∽ ;
②是否存在这样的点 ,使 是等腰三角形?若存在,请求出 的长;若不存在,请说明理由.