广东省揭阳市2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-10-16 类型:期末考试
一、单选题
-
1. -4的相反数是( )A、 B、 C、4 D、-42. 未来三年,国家将投入8450亿元用于缓解群众“看病难、看病贵”的问题.将8450亿元用科学记数法表示为( )A、0.845×104亿元 B、8.45×103亿元 C、8.45×104亿元 D、84.5×102亿元3. 一个铁制零件(正方体中间挖去一个圆柱形孔)如图放置,它的左视图是( )
 A、
A、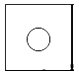 B、
B、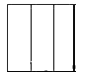 C、
C、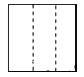 D、
D、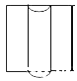 4. 一名射击爱好者5次射击的中靶环数如下:6,7,9,8,9,这5个数据的中位数是( ).A、6 B、7 C、8 D、95. 在数轴上表示不等式﹣2≤x<4,正确的是( )A、
4. 一名射击爱好者5次射击的中靶环数如下:6,7,9,8,9,这5个数据的中位数是( ).A、6 B、7 C、8 D、95. 在数轴上表示不等式﹣2≤x<4,正确的是( )A、 B、
B、 C、
C、 D、
D、 6. 下列图形中,既是中心对称图形又是轴对称图形的是( )A、
6. 下列图形中,既是中心对称图形又是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 7. 如图,下列条件不能判定△ADB∽△ABC的是( )
7. 如图,下列条件不能判定△ADB∽△ABC的是( )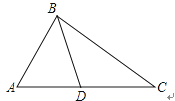 A、∠ABD=∠ACB B、∠ADB=∠ABC C、AB2=AD•AC D、8. 一元二次方程 的两根之和为( )A、 B、2 C、-3 D、39. 如图,点P是矩形ABCD的边上一动点,矩形两边长AB、BC长分别为15和20,那么P到矩形两条对角线AC和BD的距离之和是( )
A、∠ABD=∠ACB B、∠ADB=∠ABC C、AB2=AD•AC D、8. 一元二次方程 的两根之和为( )A、 B、2 C、-3 D、39. 如图,点P是矩形ABCD的边上一动点,矩形两边长AB、BC长分别为15和20,那么P到矩形两条对角线AC和BD的距离之和是( ) A、6 B、12 C、24 D、不能确定10. 如图,在同一平面直角坐标系中,一次函数y1=kx+b(k、b是常数,且k≠0)与反比例函数y2= (c是常数,且c≠0)的图象相交于A(﹣3,﹣2),B(2,3)两点,则不等式y1>y2的解集是( )
A、6 B、12 C、24 D、不能确定10. 如图,在同一平面直角坐标系中,一次函数y1=kx+b(k、b是常数,且k≠0)与反比例函数y2= (c是常数,且c≠0)的图象相交于A(﹣3,﹣2),B(2,3)两点,则不等式y1>y2的解集是( )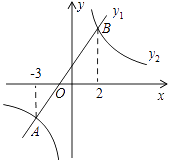 A、﹣3<x<2 B、x<﹣3或x>2 C、﹣3<x<0或x>2 D、0<x<2
A、﹣3<x<2 B、x<﹣3或x>2 C、﹣3<x<0或x>2 D、0<x<2二、填空题
-
11. 分解因式:x3﹣16x= .12. 若正多边形的每一个内角为 ,则这个正多边形的边数是 .13. 若 ,则 .14. 如图,直线l1∥l2 , 直线l3与l1、l2分别交于点A、B.若∠1=69°,则∠2的度数为 .
 15. 如图,点P是反比例函数y= (k≠0)的图象上任意一点,过点P作PM⊥x轴,垂足为M.若△POM的面积等于2,则k的值等于
15. 如图,点P是反比例函数y= (k≠0)的图象上任意一点,过点P作PM⊥x轴,垂足为M.若△POM的面积等于2,则k的值等于 16. 如图,折叠长方形的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,则EF=
16. 如图,折叠长方形的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,则EF= .17. 在平面直角坐标系中,直线l:y=x﹣1与x轴交于点A,如图所示依次作正方形A1B1C1O、正方形A2B2C2C1…、正方形AnBn∁nCn+1 , 使得点A1、A2、A3、…在直线l上,点C1、C2、C3、…在y轴正半轴上,则点B₃的坐标是 , 点Bn的坐标是 .
.17. 在平面直角坐标系中,直线l:y=x﹣1与x轴交于点A,如图所示依次作正方形A1B1C1O、正方形A2B2C2C1…、正方形AnBn∁nCn+1 , 使得点A1、A2、A3、…在直线l上,点C1、C2、C3、…在y轴正半轴上,则点B₃的坐标是 , 点Bn的坐标是 .
三、解答题
-
18. 计算:|1﹣ |+(2019﹣50 )0﹣( )﹣219. 解方程组: .20.
如图,在平行四边形ABCD中,AB<BC.
 (1)、利用尺规作图,在BC边上确定点E,使点E到边AB,AD的距离相等(不写作法,保留作图痕迹);(2)、若BC=8,CD=5,则CE= .21. 东东玩具商店用500元购进一批悠悠球,很受中小学生欢迎,悠悠球很快售完,接着又用900元购进第二批这种悠悠球,所购数量是第一批数量的1.5倍,但每套进价多了5元.
(1)、利用尺规作图,在BC边上确定点E,使点E到边AB,AD的距离相等(不写作法,保留作图痕迹);(2)、若BC=8,CD=5,则CE= .21. 东东玩具商店用500元购进一批悠悠球,很受中小学生欢迎,悠悠球很快售完,接着又用900元购进第二批这种悠悠球,所购数量是第一批数量的1.5倍,但每套进价多了5元.
(1)、求第一批悠悠球每套的进价是多少元;(2)、如果这两批悠悠球每套售价相同,且全部售完后总利润不低于25%,那么每套悠悠球的售价至少是多少元?
22. 如图,在四边形 中, , ,对角线 , 交于点 , 平分 ,过点 作 交 的延长线于点 ,连接 . (1)、求证:四边形 是菱形;(2)、若 , ,求 的长.
(1)、求证:四边形 是菱形;(2)、若 , ,求 的长.
23. 当前,“精准扶贫”工作已进入攻坚阶段,凡贫困家庭均要“建档立卡” 某初级中学七年级共有四个班,已“建档立卡”的贫困家庭的学生人数按一、二、三、四班分别记为 , , , ,现对 , , , 统计后,制成如图所示的统计图.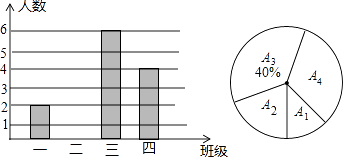 (1)、求七年级已“建档立卡”的贫困家庭的学生总人数;(2)、将条形统计图补充完整,并求出 所在扇形的圆心角的度数;
(1)、求七年级已“建档立卡”的贫困家庭的学生总人数;(2)、将条形统计图补充完整,并求出 所在扇形的圆心角的度数;
(3)、现从 , 中各选出一人进行座谈,若 中有一名女生, 中有两名女生,请用树状图表示所有可能情况,并求出恰好选出一名男生和一名女生的概率.
24. 如图,直线y=﹣x+2与反比例函数 (k≠0)的图象交于A(a,3),B(3,b)两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D. (1)、求a,b的值及反比例函数的解析式;(2)、若点P在直线y=﹣x+2上,且S△ACP=S△BDP , 请求出此时点P的坐标;(3)、在x轴正半轴上是否存在点M,使得△MAB为等腰三角形?若存在,请直接写出M点的坐标;若不存在,说明理由.25. 如图,在平面直角坐标系中,点B(12,10),过点B作x轴的垂线,垂足为A.作y轴的垂线,垂足为C.点D从O出发,沿y轴正方向以每秒1个单位长度运动;点E从O出发,沿x轴正方向以每秒3个单位长度运动;点F从B出发,沿BA方向以每秒2个单位长度运动.当点E运动到点A时,三点随之停止运动,运动过程中△ODE关于直线DE的对称图形是△O′DE,设运动时间为t.
(1)、求a,b的值及反比例函数的解析式;(2)、若点P在直线y=﹣x+2上,且S△ACP=S△BDP , 请求出此时点P的坐标;(3)、在x轴正半轴上是否存在点M,使得△MAB为等腰三角形?若存在,请直接写出M点的坐标;若不存在,说明理由.25. 如图,在平面直角坐标系中,点B(12,10),过点B作x轴的垂线,垂足为A.作y轴的垂线,垂足为C.点D从O出发,沿y轴正方向以每秒1个单位长度运动;点E从O出发,沿x轴正方向以每秒3个单位长度运动;点F从B出发,沿BA方向以每秒2个单位长度运动.当点E运动到点A时,三点随之停止运动,运动过程中△ODE关于直线DE的对称图形是△O′DE,设运动时间为t. (1)、用含t的代数式分别表示点E和点F的坐标;(2)、若△ODE与以点A,E,F为顶点的三角形相似,求t的值;(3)、当t=2时,求O′点在坐标.
(1)、用含t的代数式分别表示点E和点F的坐标;(2)、若△ODE与以点A,E,F为顶点的三角形相似,求t的值;(3)、当t=2时,求O′点在坐标.