广东省江门市新会区2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-10-16 类型:期末考试
一、单选题
-
1. 掷一枚质地均匀的骰子,骰子停止后,在下列四个选项中,可能性最大的是( )A、点数小于4 B、点数大于4 C、点数大于5 D、点数小于52. 关于x的方程x2﹣mx+6=0有一根是﹣3,那么这个方程的另一个根是( )A、﹣5 B、5 C、﹣2 D、23. 如果反比例函数y= 的图象经过点(﹣5,3),则k=( )A、15 B、﹣15 C、16 D、﹣164. 如图,把一个直角三角板△ACB绕着30°角的顶点B顺时针旋转,使得点A与CB的延长线上的点E重合,连接CD,则∠BDC的度数为( )
 A、15° B、20° C、25° D、30°5. 为了解圭峰会城九年级女生身高情况,随机抽取了圭峰会城九年级100名女生,她们的身高x(cm)统计如下:
A、15° B、20° C、25° D、30°5. 为了解圭峰会城九年级女生身高情况,随机抽取了圭峰会城九年级100名女生,她们的身高x(cm)统计如下:组别(cm)
x<150
150≤x<155
155≤x<160
160≤x<165
x≥165
频数
2
23
52
18
5
根据以上结果,随机抽查圭峰会城九年级1名女生,身高不低于155cm的概率是( )
A、0.25 B、0.52 C、0.70 D、0.756. 如图,A、D是⊙O上的两个点,BC是直径,若∠D=35°,则∠OAC的度数是( ) A、35° B、55° C、65° D、70°7. 若一元二次方程x2﹣4x﹣4m=0有两个不等的实数根,则反比例函数y= 的图象所在的象限是( )A、第一、二象限 B、第一、三象限 C、第二、四象限 D、第三、四象限8. 已知点P(x,y)在第二象限,|x|=6,|y|=8,则点P关于原点的对称点的坐标为( )A、(6,8) B、(﹣6,8) C、(﹣6,﹣8) D、(6,﹣8)9. 在同一直角坐标系中,函数y=mx+m和函数y=mx2+2x+2(m是常数,且m≠0)的图象可能是( )A、
A、35° B、55° C、65° D、70°7. 若一元二次方程x2﹣4x﹣4m=0有两个不等的实数根,则反比例函数y= 的图象所在的象限是( )A、第一、二象限 B、第一、三象限 C、第二、四象限 D、第三、四象限8. 已知点P(x,y)在第二象限,|x|=6,|y|=8,则点P关于原点的对称点的坐标为( )A、(6,8) B、(﹣6,8) C、(﹣6,﹣8) D、(6,﹣8)9. 在同一直角坐标系中,函数y=mx+m和函数y=mx2+2x+2(m是常数,且m≠0)的图象可能是( )A、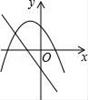 B、
B、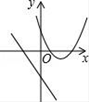 C、
C、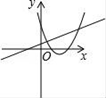 D、
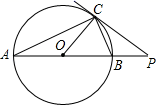
D、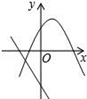 10. 已知,如图,点C、D在⊙O上,直径AB=6 ,弦AC、BD相交于点E . 若CE=BC , 则阴影部分面积为( )
10. 已知,如图,点C、D在⊙O上,直径AB=6 ,弦AC、BD相交于点E . 若CE=BC , 则阴影部分面积为( )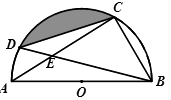 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 经过某十字路口的汽车,它可能直行,也可能向左转或向右转,假设这三种可能性大小相同,那么两辆汽车经过这个十字路口,一辆向左转,一辆向右转的概率是 .12. 反比例函数y=﹣ 的图象与一次函数y=﹣x+5的图象相交,其中一个交点坐标为(a,b),则 = .13. 已知一元二次方程ax2+bx+c=0的两根为﹣5和3,则二次函数y=ax2+bx+c图象对称轴是直线 .14. 将含有 30°角的直角三角板 OAB 如图放置在平面直角坐标系中,OB 在 x轴上,若 OA=2,将三角板绕原点 O 顺时针旋转 75°,则点 A 的对应点 A′ 的坐标为 .
 15. 如图,一次函数 的图象在第一象限与反比例函数 的图象相交于A , B两点,当 时,x的取值范围是 ,则 .
15. 如图,一次函数 的图象在第一象限与反比例函数 的图象相交于A , B两点,当 时,x的取值范围是 ,则 . 16. 定义符号max{a,b}的含义为:当a≥b时,max{a,b}=a;当a<b时,max{a,b}=b,如:max{3,1}=3,max{﹣3,2}=2,则方程max{x,﹣x}=x2﹣6的解是 .
16. 定义符号max{a,b}的含义为:当a≥b时,max{a,b}=a;当a<b时,max{a,b}=b,如:max{3,1}=3,max{﹣3,2}=2,则方程max{x,﹣x}=x2﹣6的解是 .三、解答题
-
17. 如图,四边形ABCD是⊙O的内接四边形,∠AOC=116°,则∠ADC的角度是 .
 18. 解方程:3x(2x+1)=4x+2.19. 已知点M(2,a)在反比例函数y= (k≠0)的图象上,点M关于原点中心对称的点N在一次函数y=﹣2x+8的图象上,求此反比例函数的解析式.20. 如图,已知△ABC与△A′B′C′关于点O成中心对称,点A的对称点为点A′,请你用尺规作图的方法,找出对称中心O,并作出△A′B′C′.(要求:尺规作图,保留作图痕迹,不写作法).
18. 解方程:3x(2x+1)=4x+2.19. 已知点M(2,a)在反比例函数y= (k≠0)的图象上,点M关于原点中心对称的点N在一次函数y=﹣2x+8的图象上,求此反比例函数的解析式.20. 如图,已知△ABC与△A′B′C′关于点O成中心对称,点A的对称点为点A′,请你用尺规作图的方法,找出对称中心O,并作出△A′B′C′.(要求:尺规作图,保留作图痕迹,不写作法). 21. 网络购物已成为新的消费方式,催生了快递行业的高速发展,某小型的快递公司,今年5月份与7月份完成快递件数分别为5万件和5.832份万件,假定每月投递的快递件数的增长率相同.(1)、求该快递公司投递的快递件数的月平均增长率;(2)、如果每个快递小哥平均每月最多可投递0.8万件,公司现有8个快递小哥,按此快递增长速度,不增加人手的情况下,能否完成今年9月份的投递任务?22. 在一个不透明的盒子里,装有四个分别标有数字2、3、4、6的乒乓球,它们的形状、大小、颜色、质地完全相同,耀华同学先从盒子里随机取出一个小球,记为数字x,不放回,再由洁玲同学随机取出另一个小球,记为数字y,(1)、用树状图或列表法表示出坐标(x,y)的所有可能出现的结果;(2)、求取出的坐标(x,y)对应的点落在反比例函数y= 图象上的概率.23. 一艘运沙船装载着5000m3沙子,到达目的地后开始卸沙,设平均卸沙速度为v(单位:m3/小时),卸沙所需的时间为t(单位:小时).(1)、求v关于t的函数表达式,并用列表描点法画出函数的图象;(2)、若要求在20小时至25小时内(含20小时和25小时)卸完全部沙子,求卸沙的速度范围.
21. 网络购物已成为新的消费方式,催生了快递行业的高速发展,某小型的快递公司,今年5月份与7月份完成快递件数分别为5万件和5.832份万件,假定每月投递的快递件数的增长率相同.(1)、求该快递公司投递的快递件数的月平均增长率;(2)、如果每个快递小哥平均每月最多可投递0.8万件,公司现有8个快递小哥,按此快递增长速度,不增加人手的情况下,能否完成今年9月份的投递任务?22. 在一个不透明的盒子里,装有四个分别标有数字2、3、4、6的乒乓球,它们的形状、大小、颜色、质地完全相同,耀华同学先从盒子里随机取出一个小球,记为数字x,不放回,再由洁玲同学随机取出另一个小球,记为数字y,(1)、用树状图或列表法表示出坐标(x,y)的所有可能出现的结果;(2)、求取出的坐标(x,y)对应的点落在反比例函数y= 图象上的概率.23. 一艘运沙船装载着5000m3沙子,到达目的地后开始卸沙,设平均卸沙速度为v(单位:m3/小时),卸沙所需的时间为t(单位:小时).(1)、求v关于t的函数表达式,并用列表描点法画出函数的图象;(2)、若要求在20小时至25小时内(含20小时和25小时)卸完全部沙子,求卸沙的速度范围.