广东省广州市番禺区2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-10-16 类型:期末考试
一、单选题
-
1. 一元二次方程x2﹣2x﹣1=0的根是( )A、x1=1,x2=2 B、x1=﹣1,x2=﹣2 C、x1=1+ ,x2=1﹣ D、x1=1+ ,x2=1﹣2. 下列图形是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图,⊙O是△ABC的外接圆,∠BOC=100°,则∠A的度数为( )
3. 如图,⊙O是△ABC的外接圆,∠BOC=100°,则∠A的度数为( )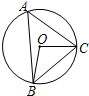 A、40° B、50° C、80° D、100°4. 抛物线y=x2﹣2x+3的顶点坐标是( )A、(1,3) B、(﹣1,3) C、(1,2) D、(﹣1,2)5. 如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的 后得到线段CD,则线段CD的长为( )
A、40° B、50° C、80° D、100°4. 抛物线y=x2﹣2x+3的顶点坐标是( )A、(1,3) B、(﹣1,3) C、(1,2) D、(﹣1,2)5. 如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的 后得到线段CD,则线段CD的长为( )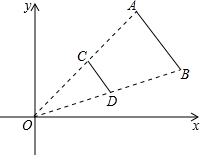 A、2 B、 C、3 D、6. 若一元二次方程kx2﹣3x﹣ =0有实数根,则实数k的取值范围是( )A、k=﹣1 B、k≥﹣1且k≠0 C、k>﹣1且k≠0 D、k≤﹣1且k≠07. 一个不透明的盒子中放入四张卡片,每张卡片上都写有一个数字,分别是﹣2,﹣1,0,1.卡片除数字不同外其它均相同,从中随机抽取两张卡片,抽取的两张卡片上数字之积为负数的概率是( )A、 B、 C、 D、8. 如图,在⊙O中,AE是直径,半径OC垂直于弦AB于D,连接BE,若AB=2 ,CD=1,则BE的长是( )
A、2 B、 C、3 D、6. 若一元二次方程kx2﹣3x﹣ =0有实数根,则实数k的取值范围是( )A、k=﹣1 B、k≥﹣1且k≠0 C、k>﹣1且k≠0 D、k≤﹣1且k≠07. 一个不透明的盒子中放入四张卡片,每张卡片上都写有一个数字,分别是﹣2,﹣1,0,1.卡片除数字不同外其它均相同,从中随机抽取两张卡片,抽取的两张卡片上数字之积为负数的概率是( )A、 B、 C、 D、8. 如图,在⊙O中,AE是直径,半径OC垂直于弦AB于D,连接BE,若AB=2 ,CD=1,则BE的长是( )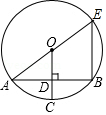 A、5 B、6 C、7 D、89. 若点A(﹣1,0)为抛物线y=﹣3(x﹣1)2+c图象上一点,则当y≥0时,x的取值范围是( )A、﹣1<x<3 B、x<﹣1或x>3 C、﹣1≤x≤3 D、x≤﹣1或x≥310. 如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为PQ,则△PQD的面积为( )
A、5 B、6 C、7 D、89. 若点A(﹣1,0)为抛物线y=﹣3(x﹣1)2+c图象上一点,则当y≥0时,x的取值范围是( )A、﹣1<x<3 B、x<﹣1或x>3 C、﹣1≤x≤3 D、x≤﹣1或x≥310. 如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为PQ,则△PQD的面积为( )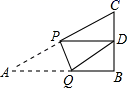 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 方程(x﹣1)(x﹣3)=0的解为 .12. 点A(﹣2,3)关于原点对称的点的坐标是 .13. 如图,已知⊙O的半径是2,点A、B、C在⊙O上,若四边形OABC为菱形,则图中阴影部分面积为 .
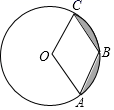 14. 将抛物线 先向右平移1个单位长度,再向上平移2个单位长度,得到的抛物线的解析式是.15. 若同时抛掷两枚质地均匀的骰子,则事件“两枚骰子朝上的点数互不相同”的概率是 .16. 如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC的中点恰好与D点重合,AB'交CD于点E,若AB=3cm,则线段EB′的长为 .
14. 将抛物线 先向右平移1个单位长度,再向上平移2个单位长度,得到的抛物线的解析式是.15. 若同时抛掷两枚质地均匀的骰子,则事件“两枚骰子朝上的点数互不相同”的概率是 .16. 如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC的中点恰好与D点重合,AB'交CD于点E,若AB=3cm,则线段EB′的长为 .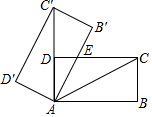
三、解答题
-
17.(1)、解方程:x(x﹣3)=x﹣3;(2)、用配方法解方程:x2﹣10x+6=018. 在如图网格图中,每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=4.
 (1)、试在图中作出△ABC以A为旋转中心,沿顺时针方向旋转90°后的图形△AB1C1;(2)、若点B的坐标为(﹣3,5),试在图中画出直角坐标系,并直接写出A、C两点的坐标;(3)、根据(2)的坐标系作出与△ABC关于原点对称的图形△A2B2C2 , 并直接写出点A2、B2、C2的坐标.19. 画出抛物线y=﹣ (x﹣1)2+5的图象(要求列表,描点),回答下列问题:(1)、写出它的开口方向,对称轴和顶点坐标;(2)、当y随x的增大而增大时,写出x的取值范围;(3)、若抛物线与x轴的左交点(x1 , 0)满足n≤x1≤n+1,(n为整数),试写出n的值.20. 如图,已知⊙O为Rt△ABC的内切圆,切点分别为D,E,F,且∠C=90°,AB=13,BC=12.
(1)、试在图中作出△ABC以A为旋转中心,沿顺时针方向旋转90°后的图形△AB1C1;(2)、若点B的坐标为(﹣3,5),试在图中画出直角坐标系,并直接写出A、C两点的坐标;(3)、根据(2)的坐标系作出与△ABC关于原点对称的图形△A2B2C2 , 并直接写出点A2、B2、C2的坐标.19. 画出抛物线y=﹣ (x﹣1)2+5的图象(要求列表,描点),回答下列问题:(1)、写出它的开口方向,对称轴和顶点坐标;(2)、当y随x的增大而增大时,写出x的取值范围;(3)、若抛物线与x轴的左交点(x1 , 0)满足n≤x1≤n+1,(n为整数),试写出n的值.20. 如图,已知⊙O为Rt△ABC的内切圆,切点分别为D,E,F,且∠C=90°,AB=13,BC=12.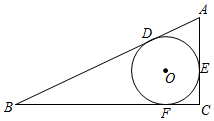 (1)、求BF的长;(2)、求⊙O的半径r.21. 端午节是我国传统佳节.小峰同学带了4个粽子(除粽馅不同外,其它均相同),其中有两个肉馅粽子、一个红枣馅粽子和一个豆沙馅粽子,准备从中任意拿出两个送给他的好朋友小悦.(1)、用树状图或列表的方法列出小悦拿到两个粽子的所有可能结果;(2)、请你计算小悦拿到的两个粽子都是肉馅的概率.22. 如图,点E,F,G,H分别位于边长为a的正方形ABCD的四条边上,四边形EFGH也是正方形,AG=x,正方形EFGH的面积为y.
(1)、求BF的长;(2)、求⊙O的半径r.21. 端午节是我国传统佳节.小峰同学带了4个粽子(除粽馅不同外,其它均相同),其中有两个肉馅粽子、一个红枣馅粽子和一个豆沙馅粽子,准备从中任意拿出两个送给他的好朋友小悦.(1)、用树状图或列表的方法列出小悦拿到两个粽子的所有可能结果;(2)、请你计算小悦拿到的两个粽子都是肉馅的概率.22. 如图,点E,F,G,H分别位于边长为a的正方形ABCD的四条边上,四边形EFGH也是正方形,AG=x,正方形EFGH的面积为y.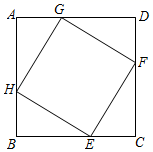 (1)、当a=2,y=3时,求x的值;(2)、当x为何值时,y的值最小?最小值是多少?23. 如图,在△ABC中,点O在边AC上,⊙O与△ABC的边BC,AB分别相切于C,D两点,与边AC交于E点,弦CF与AB平行,与DO的延长线交于M点.
(1)、当a=2,y=3时,求x的值;(2)、当x为何值时,y的值最小?最小值是多少?23. 如图,在△ABC中,点O在边AC上,⊙O与△ABC的边BC,AB分别相切于C,D两点,与边AC交于E点,弦CF与AB平行,与DO的延长线交于M点.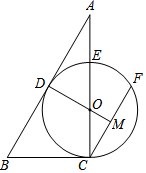 (1)、求证:点M是CF的中点;(2)、若E是 的中点,BC=a,
(1)、求证:点M是CF的中点;(2)、若E是 的中点,BC=a,①求 的弧长;
②求 的值.
24. 在△ABC中,P为边AB上一点.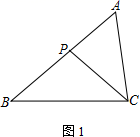
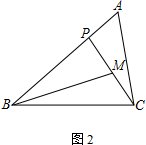
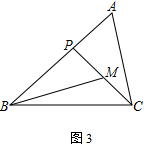 (1)、如图1,若∠ACP=∠B,求证:AC2=AP·AB;(2)、若M为CP的中点,AC=2,
(1)、如图1,若∠ACP=∠B,求证:AC2=AP·AB;(2)、若M为CP的中点,AC=2,① 如图2,若∠PBM=∠ACP,AB=3,求BP的长;
② 如图3,若∠ABC=45°,∠A=∠BMP=60°,直接写出BP的长.
25. 在平面直角坐标系中,已知抛物线y= x2+kx+c的图象经过点C(0,1),当x=2时,函数有最小值.(1)、求抛物线的解析式;(2)、直线l⊥y轴,垂足坐标为(0,﹣1),抛物线的对称轴与直线l交于点A.在x轴上有一点B,且AB= ,试在直线l上求异于点A的一点Q,使点Q在△ABC的外接圆上;(3)、点P(a,b)为抛物线上一动点,点M为坐标系中一定点,若点P到直线l的距离始终等于线段PM的长,求定点M的坐标.