广东省广州市白云区2019-2020学年九年级上学期数学期末试卷

试卷更新日期：2020-10-16 类型：期末考试

进入出卷网下载

一、单选题

1. 方程x²－4＝0的解是（）

A、x＝2 B、x＝－2 C、x＝±2 D、x＝±4

查看试题解析
2. 下列图形中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 二次函数 $y = {(x - 1)}^{2} + 2$ 的最小值是（）

A、-2 B、2 C、-1 D、1

查看试题解析
4. 一枚质地均匀的骰子，它的六个面上分别有1到6的点数．下列事件中，是不可能事件的是（）

A、掷一次这枚骰子，向上一面的点数小于5 B、掷一次这枚骰子，向上一面的点数等于5 C、掷一次这枚骰子，向上一面的点数等于6 D、掷一次这枚骰子，向上一面的点数大于6

查看试题解析
5. 已知点C为线段AB延长线上的一点，以A为圆心，AC长为半径作⊙A ，则点B与⊙A的位置关系为（）

A、点B在⊙A上 B、点B在⊙A外 C、点B在⊙A内 D、不能确定

查看试题解析
6. 两个相邻自然数的积是132．则这两个数中，较大的数是（）

A、11 B、12 C、13 D、14

查看试题解析
7. 下列抛物线中，其顶点在反比例函数y＝ $\frac{12}{x}$ 的图象上的是（）

A、y＝（x﹣4）²+3 B、y＝（x﹣4）²﹣3 C、y＝（x+2）²+1 D、y＝（x+2）²﹣1

查看试题解析
8. 如图是一个可以自由转动的转盘，转盘分成黑、白两种颜色指针的位置固定，转动的转盘停止后，指针恰好指向白色扇形的穊率为 $\frac{7}{8}$ （指针指向OA时，当作指向黑色扇形；指针指OB时，当作指向白色扇形），则黑色扇形的圆心角∠AOB＝（）

A、40° B、45° C、50° D、60°

查看试题解析
9. 一根水平放置的圆柱形输水管横截面积如图所示，其中有水部分水面宽8米，最深处水深2米，则此输水管道的半径是（）

A、4米 B、5米 C、6米 D、8米

查看试题解析
10. 在下列函数图象上任取不同两点P（x₁ ， y₁），Q（x₂ ， y₂），一定能使（x₂﹣x₁）（y₂﹣y₁）＞0成立的是（）

A、y＝﹣2x+1（x＜0） B、y＝﹣x²﹣2x+8（x＜0） C、y＝ $\frac{\sqrt{5}}{x}$ （x＞0） D、y＝2x²+x﹣6（x＞0）

查看试题解析

二、填空题

11. 在平面直角坐标系中，点P（2，﹣3）关于原点对称点P′的坐标是．

查看试题解析
12. 从甲、乙、丙三人中任选两人参加“青年志愿者”活动，甲被选中的概率为．

查看试题解析
13. 已知圆锥的底面半径是3cm，母线长是5cm，则圆锥的侧面积为cm² ．（结果保留π）

查看试题解析
14. 如图，△ABC内接于⊙O，∠ACB＝35º，则∠OAB＝º.

查看试题解析
15. 若关于x的方程x²+2x﹣m＝0（m是常数）有两个相等的实数根，则反比例函数y＝ $\frac{m}{x}$ 经过第象限．

查看试题解析
16. 如图，在正方形ABCD中，AB＝a ，点E ， F在对角线BD上，且∠ECF＝∠ABD ，将△BCE绕点C旋转一定角度后，得到△DCG ，连接FG ．则下列结论：
①∠FCG＝∠CDG；

②△CEF的面积等于 $\frac{1}{4} a^{2}$ ；

③FC平分∠BFG；

④BE²+DF²＝EF²；

其中正确的结论是．（填写所有正确结论的序号）

查看试题解析

三、解答题

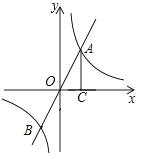
17. 解方程：x²﹣6x+8＝0．

查看试题解析
18. 如图，在同一平面直角坐标系中，正比例函数y＝2x的图象与反比例函数y＝ $\frac{k}{x}$ 的图象交于A ， B两点，过点A作AC⊥x轴，垂足为点C ， AC＝2，求k的值．

查看试题解析
19. 如图，在△ABC中，边BC与⊙A相切于点D ， ∠BAD＝∠CAD ．求证：AB＝AC ．

查看试题解析

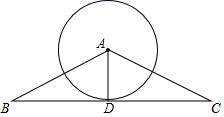20. 为了创建文明城市，增弘环保意识，某班随机抽取了8名学生（分别为A ， B ， C ， D ， E ， F ， G ， H），进行垃圾分类投放检测，检测结果如下表，其中“√”表示投放符合题意，“×”表示投放错误

学生垃圾类别	A	B	C	D	E	F	G	H
可回收物	√	×	×	√	√	×	√	√
其他垃圾	×	√	√	√	√	×	√	√
餐厨垃圾	√	√	√	√	√	√	√	√
有害垃圾	×	√	×	×	×	√	×	√

(1)、检测结果中，有几名学生正确投放了至少三类垃圾？请列举出这几名学生．

(2)、为进一步了解学生垃圾分类的投放情况，从检测结果是“有害垃圾”投放错误的学生中随机抽取2名进行访谈，求抽到学生A的概率．

查看试题解析

21. 如图，在平面直角坐标系xOy中，A（﹣2，0），B（0，3），C（﹣4，1）．以原点O为旋转中心，将△ABC顺时针旋转90°得到△A'B'C'，其中点A ， B ， C旋转后的对应点分别为点A'，B'，C'．

(1)、画出△A'B'C'，并写出点A'，B'，C'的坐标；

(2)、求经过点B'，B ， A三点的抛物线对应的函数解析式．

查看试题解析
22. 为改善生态环境，建设美丽乡村，某村规划将一块长18米，宽10米的矩形场地建设成绿化广场，如图，内部修建三条宽相等的小路，其中一条路与广场的长平行，另两条路与广场的宽平行，其余区域种植绿化，使绿化区域的面积为广场总面积的80%．

(1)、求该广场绿化区域的面积；

(2)、求广场中间小路的宽．

查看试题解析
23. 如图，在等边△ABC中，AB＝6，AD是高．

(1)、尺规作图：作△ABC的外接圆⊙O（保留作图痕迹，不写作法）

(2)、在（1）所作的图中，求线段AD ， BD与弧 $AB$ 所围成的封闭图形的面积．

查看试题解析
24. 已知抛物线y＝x²+（1﹣2a）x﹣2a（a是常数）．

(1)、证明：该抛物线与x轴总有交点；

(2)、设该抛物线与x轴的一个交点为A（m ， 0），若2＜m≤5，求a的取值范围；

(3)、在（2）的条件下，若a为整数，将抛物线在x轴下方的部分沿x轴向上翻折，其余部分保持不变，得到一个新图象G ，请你结合新图象，探究直线y＝kx+1（k为常数）与新图象G公共点个数的情况．

查看试题解析
25. 如图，AB是⊙O的直径，点C是⊙O上一点（点C不与A ， B重合），连接CA ， CB ． ∠ACB的平分线CD与⊙O交于点D ．

(1)、求∠ACD的度数；

(2)、探究CA ， CB ， CD三者之间的等量关系，并证明；

(3)、E为⊙O外一点，满足ED＝BD ， AB＝5，AE＝3，若点P为AE中点，求PO的长．

查看试题解析