广东省佛山市高明区2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-10-16 类型:期末考试
一、单选题
-
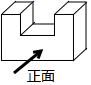
1. 如图的几何体,它的主视图是( )
 A、
A、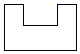 B、
B、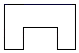 C、
C、 D、
D、 2. sin45°的值等于( )
2. sin45°的值等于( )
A、 B、 C、 D、3. 一次掷两枚质地均匀的硬币,出现两枚硬币都正面朝上的概率是( )A、 B、 C、 D、4. 已知反比例函数的图象经过点(1,2),则它的图象也一定经过( )A、(1,﹣2) B、(﹣1,2) C、(﹣2,1) D、(﹣1,﹣2)5. 已知关于x的方程x2﹣x+m=0的一个根是3,则另一个根是( )A、﹣6 B、6 C、﹣2 D、26. 已知 如图,则下列4个三角形中,与 相似的是( ) A、
A、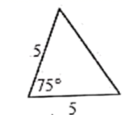 B、
B、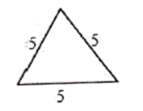 C、
C、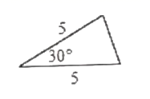 D、
D、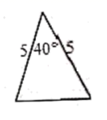 7. 如图,在菱形ABCD中,对角线AC与BD相交于点O,若AB=4,cos∠ABC= ,则BD的长为( )
7. 如图,在菱形ABCD中,对角线AC与BD相交于点O,若AB=4,cos∠ABC= ,则BD的长为( )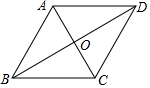 A、2 B、4 C、2 D、48. 已知关于x的方程x2﹣3x+2k=0有两个不相等的实数根,则k的取值范围是( )A、k> B、k< C、k<﹣ D、k<9. 函数y=kx﹣k(k≠0)和y=﹣ (k≠0)在同一平面直角坐标系中的图象可能是( )A、
A、2 B、4 C、2 D、48. 已知关于x的方程x2﹣3x+2k=0有两个不相等的实数根,则k的取值范围是( )A、k> B、k< C、k<﹣ D、k<9. 函数y=kx﹣k(k≠0)和y=﹣ (k≠0)在同一平面直角坐标系中的图象可能是( )A、 B、
B、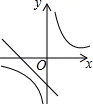 C、
C、 D、
D、 10. 如图,在△ABC中,BM⊥AC于点M , CN⊥AB于点N , P为BC边的中点,连接PM、PN、MN , 则下列结论:①PM=PN;② ;③若∠ABC=60°,则△PMN为等边三角形;④若∠ABC=45°,则BN= PC . 其中正确的是( )
10. 如图,在△ABC中,BM⊥AC于点M , CN⊥AB于点N , P为BC边的中点,连接PM、PN、MN , 则下列结论:①PM=PN;② ;③若∠ABC=60°,则△PMN为等边三角形;④若∠ABC=45°,则BN= PC . 其中正确的是( ) A、①②③ B、①②④ C、①③④ D、②③④
A、①②③ B、①②④ C、①③④ D、②③④二、填空题
-
11. 方程x2﹣9x=0的根是 .12. 在阳光下,高6m的旗杆在水平地面上的影子长为4m , 此时测得附近一个建筑物的影子长为16m , 则该建筑物的高度是m .13. 已知A(x1 , y1)B(x2 , y2)为反比例函数 图象上的两点,且x1<x2<0,则:y1y2(填“>”或“<”).
14. 某地区2017年投入教育经费2 500万元,2019年计划投入教育经费3 025万元,则2017年至2019年,该地区投入教育经费的年平均增长率为.15. 如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段 的长为 . 16. 如图,点E在正方形ABCD的边CD上.若△ABE的面积为8,CE=3,则线段BE的长为 .
16. 如图,点E在正方形ABCD的边CD上.若△ABE的面积为8,CE=3,则线段BE的长为 . 17. 如图,在Rt△ABC中,∠C=90°,AC=6,AD∥BC , DE与AB交于点F , 已知AD=4,DF=2EF , sin∠DAB= ,则线段DE= .
17. 如图,在Rt△ABC中,∠C=90°,AC=6,AD∥BC , DE与AB交于点F , 已知AD=4,DF=2EF , sin∠DAB= ,则线段DE= .
三、解答题
-
18. 解方程:x2+x﹣1=0.19. 在平面直角坐标系中,△OAB三个顶点的坐标分别为O(0,0),A(3,0),B(2,3).
 (1)、tan∠OAB=;(2)、在第一象限内画出△OA'B',使△OA'B'与△OAB关于点O位似,相似比为2:1;(3)、在(2)的条件下,S△OAB:S四边形AA′B′B= .20. 在一个不透明的袋子中,装有除颜色外都完全相同的4个红球和若干个黄球.(1)、如果从袋中任意摸出一个球是红球的概率为 ,那么袋中有黄球多少个?(2)、在(1)的条件下如果从袋中摸出一个球记下颜色后放回,再摸出一个球,用列表或画树状图的方法求出两次摸出不同颜色球的概率.21. 如图,已知菱形ABCD,AB=AC,E、F分别是BC、AD的中点,连接AE、CF.
(1)、tan∠OAB=;(2)、在第一象限内画出△OA'B',使△OA'B'与△OAB关于点O位似,相似比为2:1;(3)、在(2)的条件下,S△OAB:S四边形AA′B′B= .20. 在一个不透明的袋子中,装有除颜色外都完全相同的4个红球和若干个黄球.(1)、如果从袋中任意摸出一个球是红球的概率为 ,那么袋中有黄球多少个?(2)、在(1)的条件下如果从袋中摸出一个球记下颜色后放回,再摸出一个球,用列表或画树状图的方法求出两次摸出不同颜色球的概率.21. 如图,已知菱形ABCD,AB=AC,E、F分别是BC、AD的中点,连接AE、CF. (1)、求证:四边形AECF是矩形;(2)、若AB=6,求菱形的面积.22. 小明家所在居民楼的对面有一座大厦AB , 高为74米,为测量居民楼与大厦之间的距离,小明从自己家的窗户C处测得大厦顶部A的仰角为37°,大厦底部B的俯角为48°.
(1)、求证:四边形AECF是矩形;(2)、若AB=6,求菱形的面积.22. 小明家所在居民楼的对面有一座大厦AB , 高为74米,为测量居民楼与大厦之间的距离,小明从自己家的窗户C处测得大厦顶部A的仰角为37°,大厦底部B的俯角为48°. (1)、求∠ACB的度数;(2)、求小明家所在居民楼与大厦之间的距离.(参考数据:sin37°≈ ,cos37°≈ ,tan37°≈ ,sin48°≈ ,cos48°≈ ,tan48°≈ )23. 如图,在Rt△ABC中,∠A=90°,AB=20cm , AC=15cm , 在这个直角三角形内有一个内接正方形,正方形的一边FG在BC上,另两个顶点E、H分别在边AB、AC上.
(1)、求∠ACB的度数;(2)、求小明家所在居民楼与大厦之间的距离.(参考数据:sin37°≈ ,cos37°≈ ,tan37°≈ ,sin48°≈ ,cos48°≈ ,tan48°≈ )23. 如图,在Rt△ABC中,∠A=90°,AB=20cm , AC=15cm , 在这个直角三角形内有一个内接正方形,正方形的一边FG在BC上,另两个顶点E、H分别在边AB、AC上.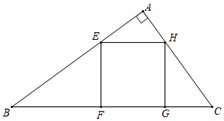 (1)、求BC边上的高;(2)、求正方形EFGH的边长.24. 如图,已知直线y=kx+b与反比例函数y= (x>0)的图象交于A(1,4)、B(4,1)两点,与x轴交于C点.
(1)、求BC边上的高;(2)、求正方形EFGH的边长.24. 如图,已知直线y=kx+b与反比例函数y= (x>0)的图象交于A(1,4)、B(4,1)两点,与x轴交于C点. (1)、求一次函数与反比例函数的解析式;(2)、根据图象直接回答:在第一象限内,当x取何值时,一次函数值大于反比例函数值?(3)、点P是y= (x>0)图象上的一个动点,作PQ⊥x轴于Q点,连接PC , 当S△CPQ= S△CAO时,求点P的坐标.25. 如图1,矩形ABCD中,AD=2,AB=3,点E , F分别在边AB , BC上,且BF=FC , 连接DE , EF , 并以DE , EF为边作▱DEFG .
(1)、求一次函数与反比例函数的解析式;(2)、根据图象直接回答:在第一象限内,当x取何值时,一次函数值大于反比例函数值?(3)、点P是y= (x>0)图象上的一个动点,作PQ⊥x轴于Q点,连接PC , 当S△CPQ= S△CAO时,求点P的坐标.25. 如图1,矩形ABCD中,AD=2,AB=3,点E , F分别在边AB , BC上,且BF=FC , 连接DE , EF , 并以DE , EF为边作▱DEFG . (1)、连接DF , 求DF的长度;(2)、求▱DEFG周长的最小值;(3)、当▱DEFG为正方形时(如图2),连接BG , 分别交EF , CD于点P、Q , 求BP:QG的值.
(1)、连接DF , 求DF的长度;(2)、求▱DEFG周长的最小值;(3)、当▱DEFG为正方形时(如图2),连接BG , 分别交EF , CD于点P、Q , 求BP:QG的值.