四川省宜宾市叙州区2019-2020学年九年级上学期数学期中试卷

试卷更新日期：2020-10-16 类型：期中考试

进入出卷网下载

一、单选题

1. 在式子 $\frac{2}{x - 1}$ ， $\frac{1}{x - 2}$ ， $\sqrt{x - 1}$ ， $\sqrt{x - 2}$ 中， $x$ 可以同时取1和2的是（）

A、 $\frac{2}{x - 1}$ B、 $\frac{1}{x - 2}$ C、 $\sqrt{x - 1}$ D、 $\sqrt{x - 2}$

查看试题解析
2. 已知最简二次根式 $\sqrt[a + b + 1]{3 a - b}$ 与 $\sqrt{12}$ 可以合并成一项，则 $a$ 、 $b$ 的值分别为（）

A、 $a = 1, b = 2$ B、 $a = - 1, b = 0$ C、 $a = 1, b = 0$ D、 $a = - 1, b = 2$

查看试题解析
3. 若 $y = \sqrt{x - 2} + \sqrt{4 - 2 x} - 3$ ，则x+y=（）

A、1 B、5 C、 $- 5$ D、 $- 1$

查看试题解析
4. 方程 $(m + 1) x^{| m - 1 |} + m x + 2 = 0$ 是关于 $x$ 的一元二次方程，则（）

A、 $m = - 1$ 或3 B、 $m = 3$ C、 $m = - 1$ D、 $m \neq - 1$

查看试题解析
5. 已知 $a$ 是方程 $2 x^{2} - 4 x - 3 = 0$ 的一个根，则代数式 $2 a^{2} - 4 a$ 的值等于（）

A、3 B、2 C、0 D、1

查看试题解析
6. 方程 $(x - 2) (x + 1) = (x + 1)$ 的解是（）

A、 $x = 2$ B、 $x = - 1$ C、 $x_{1} = 3, x_{2} = - 1$ D、 $x_{1} = - 3, x_{2} = 1$

查看试题解析
7. 如果关于x的方程x²+k²-16=0和x²-3k+12=0有相同的实数根，那么k的值是（）

A、-7 B、-7或4 C、-4 D、4

查看试题解析
8. 目前我国已建立了比较完善的经济困难学生资助体系，某校去年上半年发放给每个经济困难学生389元，今年上半年发放了438元，设每半年发放的资助金额的平均增长率为x，则下面列出的方程中正确的是（）

A、438（1+x）²=389 B、389（1+x）²=438 C、389（1+2x）=438 D、438（1+2x）=389

查看试题解析
9. 如图，AD∥BE∥CF，直线l₁、l₂与这三条平行线分别交于点A，B，C和点D，E，F.若AB＝4.5，BC＝3，EF＝2，则DE的长度是（）

A、 $\frac{4}{3}$ B、3 C、5 D、 $\frac{27}{4}$

查看试题解析
10. 如图，点D、E、F分别为 $Δ A B C$ 三边的中点，若 $Δ A B C$ 的周长为18，则 $Δ D E F$ 的周长为（）

A、8 B、9 C、10 D、11

查看试题解析
11. 如图，在平行四边形ABCD中，AC与BD相交于点O ， E是OD的中点，连接AE并延长交DC于点F ，则DF： $F C =$ （）

A、1：4 B、1：3 C、1：2 D、2：1

查看试题解析
12. 如图，矩形ABCD中，AE⊥BD于点E ， CF平分∠BCD ，交EA的延长线于点F ，且BC=4，CD=2，给出下列结论：①∠BAE=∠CAD；②∠DBC=30°；③AE= $\frac{4}{5} \sqrt{5}$ ；④AF= $2 \sqrt{5}$ ，其中正确结论的个数有（）

A、1个 B、2个 C、3个 D、4个32

查看试题解析

二、填空题

13. 已知 $\sqrt{a} - \sqrt{b} = \sqrt{5} - \sqrt{3}$ ， $\sqrt{a b} = \sqrt{15} - \sqrt{5}$ ，则 $a + b =$ .

查看试题解析
14. 计算： ${(\sqrt{5} - 2)}^{2018} {(\sqrt{5} + 2)}^{2019}$ 的结果是.

查看试题解析
15. 若1是一元二次方程 $(m + 1) x^{2} - x + m^{2} = 0$ 的一个根，则 $m =$ .

查看试题解析
16. 三角形的两边长分别是3和4，第三边长是方程 $x^{2} - 3 x - 10 = 0$ 的根，则该三角形是三角形.

查看试题解析
17. 已知 $a : b : c = 2 : 3 : 4$ ，则 $\frac{3 c^{2} - 2 b^{2}}{2 a^{2} + 3 b^{2} - c^{2}} =$ .

查看试题解析
18. 如图，△ABC是边长为2的等边三角形．取BC边中点E，作ED∥AB，EF∥AC，得到四边形EDAF，它的面积记作 $s_{1}$ ；取 $B E$ 中点 $E_{1}$ ，作 $E_{1} D_{1}$ ∥ $F B$ ， $E_{1} F_{1}$ ∥ $E F$ ，得到四边形 $E {}_{1}D_{1} F F_{1}$ ，它的面积记作 $s_{2}$ ．照此规律作下去，则 $s_{2019}$ = .

查看试题解析

三、解答题

19.

(1)、计算： $\sqrt{{(\sqrt{3} - 2)}^{2}} + \sqrt{27} (\sqrt{5 + \frac{1}{3}} - \sqrt{3})$

(2)、解方程： $2 x^{2} - 5 x - 3 = 0$

查看试题解析
20. 已知 $a = \frac{1}{\sqrt{3} - 2}, b = \frac{1}{\sqrt{3} + 2}$ ，求 $\sqrt{a^{2} + b^{2} + 4}$ 的值.

查看试题解析
21. 已知，如图所示，∠BCA=∠EDA．

求证：

(1)、△ABC∽△ADE

(2)、DF·EF=FC·FB

查看试题解析
22. 广安市某楼盘准备以每平方米6000元的均价对外销售，由于国务院有关房地产的新政策出台后，购房者持币观望，房地产开发商为了加快资金周转，对价格经过两次下调后，决定以每平方米4860元的均价开盘销售.

(1)、求平均每次下调的百分率.

(2)、某人准备以开盘价均价购买一套100平方米的住房，开发商给予以下两种优惠方案以供选择：①打9.8折销售；②不打折，一次性送装修费每平方米80元，试问哪种方案更优惠？

查看试题解析
23. 已知 $x_{1}, x_{2}$ 是关于 $x$ 的一元二次方程 $x^{2} - 2 (m + 1) x + m^{2} + 5 = 0$ 的两个实数根.

(1)、求m的取值范围；

(2)、若 $(x_{1} - 1) (x_{2} - 1) = 28$ ，求 $m$ 的值；

查看试题解析
24. 如图，在△ABC中，点D在BC边上，∠DAC＝∠B．点E在AD边上，CD＝CE．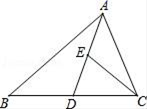

(1)、求证：△ABD∽△CAE；

(2)、若AB＝6，AC＝ $\frac{9}{2}$ ，BD＝2，求AE的长．

查看试题解析
25. 如图，四边形ABCD中，AC平分∠DAB，∠ADC=∠ACB=90º，E为AB的中点，求证：

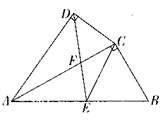(1)、AC²=AB·AD；

(2)、CE∥AD．

查看试题解析
26. 如图1，矩形ABCD的一条边AD=8，将矩形ABCD折叠，使得顶点B落在CD边上的P点处，已知折痕与边BC交于点O，连结AP、OP、OA．

(1)、求证：△OCP∽△PDA；

(2)、若△OCP与△PDA的面积比为1：4，求边AB的长；

(3)、如图2，擦去折痕AO、线段OP，连结BP．动点M在线段AP上（点M与点P、A不重合），动点N在线段AB的延长线上，且BN=PM，连结MN交PB于点F，作ME⊥BP于点E．探究：当点M、N在移动过程中，线段EF与线段PB有何数量关系？并说明理由．

查看试题解析