四川省宜宾市翠屏区2019-2020学年九年级上学期数学期中试卷

试卷更新日期：2020-10-16 类型：期中考试

进入出卷网下载

一、单选题

1. 若式子 $\sqrt{x - 1}$ 在实数范围内有意义，则x的取值范围是（）

A、x≠1 B、x＞1 C、x≥1 D、x≤1

查看试题解析
2. 下列计算结果正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $3 \sqrt{2} - \sqrt{2} = 3$ C、 $\sqrt{2} \times \sqrt{5} = \sqrt{10}$ D、 $\frac{\sqrt{2}}{\sqrt{5}} = 5 \sqrt{10}$

查看试题解析
3. 下列四组线段（单位：㎝）中，不能成比例的是（）

A、a=4，b=4，c=5，d=10 B、a=3，b=6，c=2，d=4 C、a=1，b= $\sqrt{2}$ ，c= $\sqrt{6}$ ，d= $\sqrt{3}$ D、a=2，b= $\sqrt{5}$ ，c= $\sqrt{15}$ ，d=2 $\sqrt{3}$

查看试题解析
4. 方程 $x^{2} + 6 x + 9 = 0$ 的根的情况是（）

A、有两个相等实数根 B、有两个不相等实数根 C、有一个实数根 D、没有实数根

查看试题解析
5. 实数a在数轴上的位置如图所示，则 $\sqrt{{(2 a - 3)}^{2}} + \sqrt{{(a - 15)}^{2}}$ 化简后为（）

A、-15 B、a+12 C、2a-15 D、无法确定

查看试题解析
6. 已知m、n是方程x²+3x-2=0的两个实数根，则m²+4m+n+2mn的值为（）

A、-5 B、 $- 1$ C、5 D、0

查看试题解析
7. 已知x、y为实数，且 $\sqrt{x - 1}$ +(y−2)²＝0，则x-y的值是（）

A、-3 B、1 C、-1 D、8

查看试题解析
8. 若 $\frac{a}{b} = \frac{c}{d} = \frac{e}{f} = 0.5$ ，则 $\frac{3 a - 2 c + e}{3 b - 2 d + f}$ 的值为（）

A、0.5 B、1 C、1.5 D、2

查看试题解析
9. 下列说法中正确的是（）

A、两个等腰三角形相似 B、有一个内角是30°的两个直角三角形相似 C、有一个锐角是30°的两个等腰三角形相似 D、两个直角三角形相似

查看试题解析
10.
如图，F是平行四边形ABCD对角线BD上的点，BF：FD=1：3，则BE：EC=（　　）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{2}{3}$ D、 $\frac{1}{4}$

查看试题解析
11. 如图，在矩形ABCD中，E、F分别是DC、BC边上的点，且∠AEF=90°，则下列结论正确的是（）．

A、△ABF∽△AEF B、△ABF∽△CEF C、△CEF∽△DAE D、△DAE∽△BAF

查看试题解析
12. 如图，在钝角三角形ABC中，AB=6cm，AC=12cm，动点D从A点出发到B点止，动点E从C点出发到A点止．点D运动的速度为1cm/秒，点E运动的速度为2cm/秒．如果两点同时运动，那么当以点A、D、E为顶点的三角形与△ABC相似时，运动的时间是（）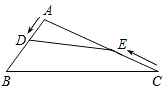

A、3秒或4.8秒 B、3秒 C、4.5秒 D、4.5秒或4.8秒

查看试题解析

二、填空题

13. 计算 $\sqrt{8} - \sqrt{2}$ 的结果是．

查看试题解析
14. 若y= $\sqrt{3 x - 6} + \sqrt{6 - 3 x} + x^{3}$ ，则10x+2y的平方根为．

查看试题解析
15. 一元二次方程 $2 x^{2} = 5 x$ 的解是．

查看试题解析
16. 已知三角形两边的长是2和3，第三边的长是方程x²﹣6x+8＝0的根，则该三角形的周长是．

查看试题解析
17. 已知：如图，在Rt△ABC中，∠ACB=90°，CD⊥AB于D ， AD=2，BD=8，那么CD= ．

查看试题解析
18. 设 $m$ 是不小于﹣1的实数，关于x的方程 $x^{2} + 2 (m - 2) x + m^{2} - 3 m + 3 = 0$ 有两个不相等的实数根 $x_{1} ， x_{2}$ ，令T= $\frac{m x_{1}}{1 - x_{1}} + \frac{m x_{2}}{1 - x_{2}}$ ，则T的取值范围是．

查看试题解析

三、解答题

19. 计算或解方程

(1)、计算： ${(\frac{1}{2})}^{- 2} - {(\sqrt{3} - π)}^{0} - \frac{\sqrt{20} - \sqrt{15}}{\sqrt{5}} - \sqrt{12}$ ．

(2)、解方程： $9 x^{2} - 6 x + 1 = 0$ ．

查看试题解析
20. 先化简再计算： $\frac{x^{2} - 1}{x^{2} + x} \div (x - \frac{2 x - 1}{x})$ ，其中x是一元二次方程 $x^{2} - 2 x - 2 = 0$ 的正数根.

查看试题解析
21. 已知关于x的一元二次方程x²-（2m+3）x+m²+2=0．

(1)、若方程有实数根，求实数m的取值范围；

(2)、若方程的两个根分别为x₁、x₂ ，且满足x₁²+x₂²=31+x₁x₂ ，求实数m的值．

查看试题解析
22. 如图，点D、E分别在 $△ A B C$ 的边AB、AC上，若 $∠ A = 40^{\circ}$ ， $∠ B = 65^{\circ}$ ， $∠ A E D = 75^{\circ}$ ．

(1)、求证： $△ A D E$ ∽ $△ A B C$ ；

(2)、已知，AD： $B D = 2$ ：3， $A E = 3$ ，求AC的长．

查看试题解析
23. 某商场将某种商品的售价从原来的每件80元经两次调价后调至每件64.8元．

(1)、若该商店两次两次调价的降价率相同，求这个降价率；

(2)、经调查，该商品每降价0.2元，即可多销售10件．若该商品原来每月可销售500件，那么两次调价后，每月可销售该商品多少件？

查看试题解析
24. 已知关于x的一元二次方程（a+c）x²+2bx+（a﹣c）=0，其中a、b、c分别为△ABC三边的长．

(1)、如果x=﹣1是方程的根，试判断△ABC的形状，并说明理由；

(2)、如果方程有两个相等的实数根，试判断△ABC的形状，并说明理由；

(3)、如果△ABC是等边三角形，试求这个一元二次方程的根．

查看试题解析
25. 如图，在平面直角坐标系中，点A、C分别在x轴、y轴上，四边形ABCO为矩形，AB=16，点D与点A关于y轴对称，AB：BC=4：3，点E、F分别是线段AD、AC上的动点（点E不与点A、D重合），且∠1=∠2．

(1)、求AC的长和点D的坐标；

(2)、求证：△AEF∽△DCE；

(3)、当△EFC为等腰三角形时，求点E的坐标．

查看试题解析