四川省遂宁市蓬溪县2019-2020学年九年级上学期数学期中试卷
试卷更新日期:2020-10-16 类型:期中考试
一、单选题
-
1. 下列代数式中,属于二次根式的为( )A、 B、 C、 D、2. 已知(x-1)2+ =0,则(x+y)2的算术平方根是( )A、±1 B、1 C、-1 D、03. 下列方程中,是关于x的一元二次方程的为( )A、 ﹣2=0 B、x3+2x=(x﹣1)(x﹣2) C、ax2+bx+c=0 D、(a2+1)x2=04. 关于x的一元二次方程 有一个根是 ,则A、1 B、-1 C、±1 D、05. 某超市7月份的营业额是200万元,第三季度的营业额共1000万元,如果每月的增长率都是x,根据题意列出的方程应该是( )A、200(1+x)2=1000 B、200(1+2x)=1000 C、200+200(1+x)+200(1+x)2=1000 D、200(1+3x)=10006. 已知x、y都是实数,且(x2+y2)(x2+y2+2)﹣3=0,那么x2+y2的值是( )A、﹣3 B、1 C、﹣3或1 D、﹣1或37. 画在图纸上的某一零件的长度是32mm , 如果比例尺是1:15,则该零件的实际长度是( )A、 mm B、480mm C、48mm D、408mm8. 下列说法中正确的是( )A、所有的矩形都相似 B、所有的菱形都相似 C、所有的正方形都相似 D、所有的等腰梯形都相似9. 若 ≠0,则下列各式中正确的是( )A、 = B、2x=3y=4z C、 =1 D、 =10. 若 是一元二次方程 的两根,则 ( )A、-8 B、32 C、16 D、4011. 如图,棋盘上若“将”位于(2,﹣2),“象”位于(4,﹣2),则“炮”位于( )
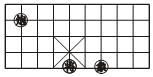 A、(﹣2,1) B、(﹣1,2) C、(﹣1,1) D、(﹣2,2)12. 在梯形ABCD中,AB∥CD , CE平分∠BCD , CE⊥AD于E , DE=2AE . 若△CED面积为1,则四边形ABCE的面积为( )A、 B、 C、 D、13. 已知a、b满足a2﹣6a+2=0,b2﹣6b+2=0,则 =( )A、﹣6 B、2 C、16 D、16或214. 若n(n≠0)是关于x的方程x2+mx+2n=0的根,则m+n的值为( )A、1 B、2 C、-1 D、-215. 如图,已知AD是△ABC的中线,AE=EF=FC,下面给出三个关系式:①AG:AD=1:2;②GE:BE=1:3③BE:BG=4:3,其中正确的是( )
A、(﹣2,1) B、(﹣1,2) C、(﹣1,1) D、(﹣2,2)12. 在梯形ABCD中,AB∥CD , CE平分∠BCD , CE⊥AD于E , DE=2AE . 若△CED面积为1,则四边形ABCE的面积为( )A、 B、 C、 D、13. 已知a、b满足a2﹣6a+2=0,b2﹣6b+2=0,则 =( )A、﹣6 B、2 C、16 D、16或214. 若n(n≠0)是关于x的方程x2+mx+2n=0的根,则m+n的值为( )A、1 B、2 C、-1 D、-215. 如图,已知AD是△ABC的中线,AE=EF=FC,下面给出三个关系式:①AG:AD=1:2;②GE:BE=1:3③BE:BG=4:3,其中正确的是( ) A、①②③ B、①② C、②③ D、①③16. 如图,在△ABC中,DE∥FG∥BC , 且AD:DF:FB=1:2:3,则S△ADE:S四边形DFGE:S四边形FBCG等于( )
A、①②③ B、①② C、②③ D、①③16. 如图,在△ABC中,DE∥FG∥BC , 且AD:DF:FB=1:2:3,则S△ADE:S四边形DFGE:S四边形FBCG等于( )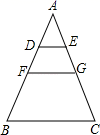 A、1:9:36 B、1:4:9 C、1:8:27 D、1:8:36
A、1:9:36 B、1:4:9 C、1:8:27 D、1:8:36二、填空题
-
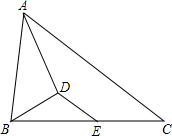
17. 若y= ,则x+y= .18. 已知线段AB=2,点C为AB的黄金分割点,且AC<BC , 那么BC= .19. 如果关于x的方程x2﹣4x+m2=0有两个相等的实数根,那么m= .20. 两个相似三角形周长的差是4,对应中线的比是4:5,那么较大三角形的周长是 .21. 如图:△ABC中,AB=4,AC=6,AD平分∠BAC , BD⊥AD , E是BC中点,那么DE= .
 22. 已知a、b为有理数,m、n分别表示 的整数部分和小数部分,且amn+bn2=1,则2a+b= .
22. 已知a、b为有理数,m、n分别表示 的整数部分和小数部分,且amn+bn2=1,则2a+b= .
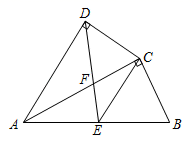
23. 如图,D是AC上一点,BE∥AC , BE=AD , AE分别交BD、BC于点F、G , ∠1=∠2.若DF=8,FG=4,则GE= .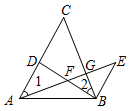 24. 在平面直角坐标系中,将线段AB平移到A′B′,若点A、B、A′的坐标分别是(-2,0),(0,3),(2,1),则点B′的坐标是
24. 在平面直角坐标系中,将线段AB平移到A′B′,若点A、B、A′的坐标分别是(-2,0),(0,3),(2,1),则点B′的坐标是
三、解答题
-
25. 计算:(1)、(2)、( )( )﹣( )226. 解方程:(1)、 ;(2)、 (用配方法);(3)、 (用公式法);(4)、27. 先化简,再求值:( ) ,其中x= ﹣1.28. 如图,四边形DEFG是△ABC的内接正方形,D、G分别在AB、AC上,E、F在BC上,AH是△ABC的高,已知BC=20,AH=16,求正方形DEFG的边长.
 29. 如图所示,在宽为 ,长为 的矩形耕地上,修筑同样宽的三条道路(互相垂直),把耕地分成大小不等的六块试验田,要使试验田的面积为 ,道路应为多宽?
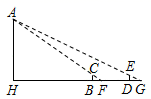
29. 如图所示,在宽为 ,长为 的矩形耕地上,修筑同样宽的三条道路(互相垂直),把耕地分成大小不等的六块试验田,要使试验田的面积为 ,道路应为多宽? 30. 如图,小明要测量操场旗杆高度AH . 立两根高1米的标杆BC和DE , 两竿相距BD=15米,D、B、H成一线,小明从BC退行2米到F , 着地观察A , A、C、F三点共线;从DE退行3米步到G , 从G看A , A、E、G三点也共线.请你帮小明算出旗杆的高度AH及HB的距离.
30. 如图,小明要测量操场旗杆高度AH . 立两根高1米的标杆BC和DE , 两竿相距BD=15米,D、B、H成一线,小明从BC退行2米到F , 着地观察A , A、C、F三点共线;从DE退行3米步到G , 从G看A , A、E、G三点也共线.请你帮小明算出旗杆的高度AH及HB的距离.