四川省南充市嘉陵区2019-2020学年九年级上学期数学期中试卷

试卷更新日期：2020-10-16 类型：期中考试

进入出卷网下载

一、单选题

1. 下列图形中，是轴对称图形，但不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若关于x的一元二次方程x²﹣2x+m=0有两个不相等的实数根，则m的取值范围是（）

A、m＜﹣1 B、m＜1 C、m＞﹣1 D、m＞1

查看试题解析
3. 抛物线y=（x+2）²﹣3可以由抛物线y=x²平移得到，则下列平移过程正确的是（）

A、先向左平移2个单位，再向上平移3个单位 B、先向左平移2个单位，再向下平移3个单位 C、先向右平移2个单位，再向下平移3个单位 D、先向右平移2个单位，再向上平移3个单位

查看试题解析
4. 抛物线y＝－2x²＋1的对称轴是（）

A、直线 $x= \frac{1}{2}$ B、直线 $x= - \frac{1}{2}$ C、y轴 D、直线x＝2

查看试题解析
5. 三角形两边的长分别是8和6，第三边的长是方程x²﹣12x+20=0的一个实数根，则三角形的周长是（）

A、24 B、26或16 C、26 D、16

查看试题解析
6. 上海世博会的某纪念品原价168元，连续两次降价a%后售价为128元，下面所列方程中正确的是（）

A、168(1＋a%)²＝128 B、168(1－a%)²＝128 C、168(1－2a%)＝128 D、168(1－a2%)＝128

查看试题解析
7. 若x＝－2是关于x的一元二次方程x²＋ $\frac{3}{2}$ ax－a²＝0的一个根，则a的值为（）

A、－1或4 B、－1或－4 C、1或－4 D、1或4

查看试题解析
8. 已知，α、β是关于x的一元二次方程x²+4x﹣1=0的两个实数根，则α+β的值是（）

A、﹣4 B、4 C、4或﹣4 D、﹣ $\frac{1}{4}$

查看试题解析
9. 如图，在 $Δ A B C$ 中， $∠ C A B = 65 °$ ，将 $Δ A B C$ 在平面内绕点 $A$ 旋转到 $Δ A B^{'} C^{'}$ 的位置，使 $C C^{'} ∥ A B$ ，则旋转角的度数为（）

A、 $35 °$ B、 $40 °$ C、 $65 °$ D、 $50 °$

查看试题解析
10. 抛物线y=ax²+bx+c的顶点为D（﹣1，2），与x轴的一个交点A在点（﹣3，0）和（﹣2，0）之间，其部分图象如图，则以下结论：①b²﹣4ac＜0；②a+b+c＜0；③c﹣a=2；④方程ax²+bx+c﹣2=0有两个相等的实数根．其中正确结论的个数为（）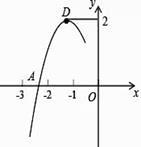

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

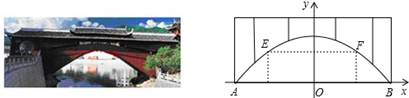
11. 已知x₁ ， x₂是方程x²-3x-1=0的两根，则 $\frac{1}{x_{1}} + \frac{1}{x_{2}}$ = ．

查看试题解析
12. 关于x的方程（m﹣3） $x^{m^{2} - 7}$ ﹣x=5是一元二次方程，则m= ．

查看试题解析
13. 已知方程x²+mx+3=0的一个根是1，则它的另一个根是．

查看试题解析
14. 已知某种礼炮的升空高度h(m)与飞行时间t(s)的关系式是 $h = - \frac{5}{2} t^{2} + 20 t + 1$ .若此礼炮在升空到最高处时引爆，则引爆需要的时间为.

查看试题解析
15. 廊桥是我国古老的文化遗产 $.$ 如图，是某座抛物线型的廊桥示意图，已知抛物线的函数表达式为 $y = - \frac{1}{40} x^{2} + 10$ ，为保护廊桥的安全，在该抛物线上距水面AB高为8米的点E，F处要安装两盏警示灯，则这两盏灯的水平距离EF是米 $. ($ 精确到1米 $)$

查看试题解析
16. 如图，在平面直角坐标系中，点 $A$ 在抛物线 $y = x^{2} - 2 x + 2$ 上运动，过点 $A$ 作 $A C ⊥ x$ 轴于点 $C$ ，以 $A C$ 为对角线作矩形 $A B C D ，$ 连结 $B D ，$ 则对角线 $B D$ 的最小值为．

查看试题解析

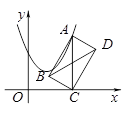
三、解答题

17. 解方程：

(1)、x²﹣7x+6＝0

(2)、（x﹣2）（x﹣5）＝﹣2

(3)、y²+6y＝1

查看试题解析
18. 关于x的一元二次方程x²+kx﹣6＝0的一个根是3，求它的另一个根和k的值．

查看试题解析
19. 已知在平面直角坐标系内，抛物线y＝x²﹣bx+6经过x轴上两点A，B，点B的坐标为（3，0），与y轴相交于点C．

(1)、求抛物线的解析式；

(2)、求△ABC的面积．

查看试题解析
20. 已知：△ABC在坐标平面内，三个顶点的坐标分别为A（0，3），B（3，4），C（2，2）．（正方形网格中，每个小正方形的边长是1个单位长度）．

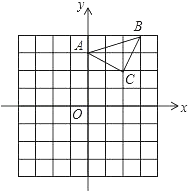(1)、作出△ABC绕点A顺时针方向旋转90°后得到的△A₁B₁C₁ ，并直接写出C₁点的坐标；

(2)、作出△ABC关于原点O成中心对称的△A₂B₂C₂ ，并直接写出B₂的坐标．

查看试题解析
21. 已知关于x的一元二次方程：x²﹣（m﹣3）x﹣m=0．

(1)、试判断原方程根的情况；

(2)、若抛物线y=x²﹣（m﹣3）x﹣m与x轴交于A（x₁ ， 0），B（x₂ ， 0）两点，则A，B两点间的距离是否存在最大或最小值？若存在，求出这个值；若不存在，请说明理由．（友情提示：AB=|x₂﹣x₁|）

查看试题解析
22. 如图，点P是正方形ABCD内一点，点P到点A，B和D的距离分别为1，2 $\sqrt{2}$ ， $\sqrt{10}$ .△ADP沿点A旋转至△ABP′，连接PP′，并延长AP与BC相交于点Q.

(1)、求证：△APP′是等腰直角三角形；

(2)、求∠BPQ的大小.

查看试题解析
23. 某衬衣店将进价为30元的一种衬衣以40元售出，平均每月能售出600件，调查表明：这种衬衣售价每上涨1元，其销售量将减少10件．

(1)、写出月销售利润y（单位：元）与售价x（单位：元/件）之间的函数解析式．

(2)、当销售价定为45元时，计算月销售量和销售利润．

(3)、当销售价定为多少元时会获得最大利润？求出最大利润．

查看试题解析
24. 已知二次函数 $y_{1} = x^{2} - 6 x + 9 - t^{2}$ 和一次函数 $y_{2} = - 2 x - 2 t + 6$ ．

(1)、当t=0时，试判断二次函数 $y_{1}$ 的图象与x轴是否有公共点，如果有，请写出公共点的坐标；

(2)、若二次函数 $y_{1}$ 的图象与x轴的两个不同公共点，且这两个公共点间的距离为8，求t的值；

(3)、求证：不论实数t取何值，总存在实数x，使 $y_{1}$ ≥ $t y_{2}$ ．

查看试题解析
25. 在平面直角坐标系中，抛物线 $y = x^{2} - 6 m x + 5$ 与y轴的交点为A ，与x轴的正半轴分别交于点B（b ， 0），C（c ， 0）.

(1)、当b=1时，求抛物线相应的函数表达式；

(2)、当b=1时，如图，E（t ， 0）是线段BC上的一动点，过点E作平行于y轴的直线l与抛物线的交点为P ．求△APC面积的最大值；

(3)、当c =b+n.时，且n为正整数.线段BC（包括端点）上有且只有五个点的横坐标是整数，求b的值.

查看试题解析