四川省广元市苍溪县2019-2020学年九年级上学期数学期中试卷
试卷更新日期:2020-10-16 类型:期中考试
一、单选题
-
1. 下列方程中是一元二次方程的是( )A、 B、 C、 D、2. 下列图形中既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3.
3.如图,⊙O的弦AB=8,M是AB的中点,且OM=3,则⊙O的半径等于( )
 A、8 B、4 C、10 D、54. 如图,将30°的三角尺以直角顶点A为旋转中心顺时针旋转,使点C落在边BC的C'处,则其旋转角的大小为( )
A、8 B、4 C、10 D、54. 如图,将30°的三角尺以直角顶点A为旋转中心顺时针旋转,使点C落在边BC的C'处,则其旋转角的大小为( ) A、30° B、60° C、90° D、150°5. 方程x2+17=8x的根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、有两个实数根 D、没有实数根6. 已知等腰三角形的腰和底的长分别是一元二次方程x2﹣6x+8=0的根,则该三角形的周长为( )A、8 B、10 C、8或10 D、127. 抛物线y=2(x-1)2+c过(-2,y1),(0,y2), ( ,y3)三点,则 大小关系是( )A、 B、 C、 D、8. 已知x1 , x2是一元二次方程x2-6x- 15=0的两个根,则x1+x2等于( )A、-6 B、6 C、-15 D、159. 抛物线y= ax2+bx+c(a≠0)对称轴为直线x=1,与x轴的一个交点坐标为(-1,0),与y轴交点为(0,3),其部分图象如图所示,则下列结论错误的是( )
A、30° B、60° C、90° D、150°5. 方程x2+17=8x的根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、有两个实数根 D、没有实数根6. 已知等腰三角形的腰和底的长分别是一元二次方程x2﹣6x+8=0的根,则该三角形的周长为( )A、8 B、10 C、8或10 D、127. 抛物线y=2(x-1)2+c过(-2,y1),(0,y2), ( ,y3)三点,则 大小关系是( )A、 B、 C、 D、8. 已知x1 , x2是一元二次方程x2-6x- 15=0的两个根,则x1+x2等于( )A、-6 B、6 C、-15 D、159. 抛物线y= ax2+bx+c(a≠0)对称轴为直线x=1,与x轴的一个交点坐标为(-1,0),与y轴交点为(0,3),其部分图象如图所示,则下列结论错误的是( ) A、a-b+c=0 B、关于x的方程ax2+bx+c- 3=0有两个不相等的实数根 C、abc>0 D、当y>0时,-1<x<310. 二次函数y=ax2 +bx+c的图象如图所示,那么一次函数y=ax-bc的图象大致是( )
A、a-b+c=0 B、关于x的方程ax2+bx+c- 3=0有两个不相等的实数根 C、abc>0 D、当y>0时,-1<x<310. 二次函数y=ax2 +bx+c的图象如图所示,那么一次函数y=ax-bc的图象大致是( ) A、
A、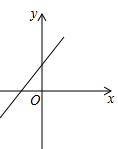 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 点A(﹣2,3)关于原点对称的点的坐标是 .12. 已知m是关于x的方程x2-2x-1=0的一个根,则2m2- 4m=.13. 与抛物线y=2(x﹣4)2﹣1,关于x轴对称的抛物线的解析式为 .14. 如图,在Rt△ABC中,∠C=90°.点O是AB的中点,边AC=6,将边长足够大的三角板的直角顶点放在点O处,将三角板绕点O旋转,始终保持三角板的直角边与AC相交,交点为点E , 另条直角边与BC相交,交点为D , 则等腰直角三角板的直角边被三角板覆盖部分的两条线段CD与CE的长度之和为 .

三、解答题
-
15. 如图,⊙O的直径为10cm,弦AB=8cm,P是弦AB上的一个动点,求OP的长度范围.
 16. 用配方法解方程:2 +1=317. 已知关于x的方程 .(1)、当该方程的一个根为1时,求a的值及该方程的另一根;(2)、求证:不论a取何实数,该方程都有两个不相等的实数根.18. 初三年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面高 m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m,设篮球运行的轨迹为抛物线,篮圈距地面3m.
16. 用配方法解方程:2 +1=317. 已知关于x的方程 .(1)、当该方程的一个根为1时,求a的值及该方程的另一根;(2)、求证:不论a取何实数,该方程都有两个不相等的实数根.18. 初三年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面高 m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m,设篮球运行的轨迹为抛物线,篮圈距地面3m.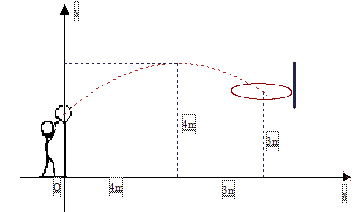 (1)、建立如图所示的平面直角坐标系,求抛物线的解析式并判断此球能否准确投中?(2)、此时,若对方队员乙在甲前面1m处跳起盖帽拦截,已知乙的最大摸高为3.1m,那么他能否获得成功?
(1)、建立如图所示的平面直角坐标系,求抛物线的解析式并判断此球能否准确投中?(2)、此时,若对方队员乙在甲前面1m处跳起盖帽拦截,已知乙的最大摸高为3.1m,那么他能否获得成功?
19. 某机械公司经销一种零件,已知这种零件的成本为每件20元,调查发现当销售价为24元,平均每天能售出32件,而当销售价每上涨2元,平均每天就少售出4件.(1)、若公司每天的销售价为x元,则每天的销售量为多少?(2)、如果物价部门规定这种零件的销售价不得高于每件28元,该公司想要每天获得150元的销售利润,销售价应当为多少元?20. 据农业农村部新闻部办公室2018年10月15日消息,江宁省发现疑似非洲猪瘟疫情,此次猪瘟疫情发病急,蔓延速度快.当政府和企业迅速进行了猪瘟疫情排查和处置,在疫情排查过程中,某农场第一天发现3头生猪发病,两天后发现共有192头生猪发病,(1)、求每头发病生猪平均每天传染多少头生猪?(2)、若疫情得不到有效控制,3天后生猪发病头数会超过1500头吗?21. 已知:如图,二次函数y=x2+(2k-1)x+k+1的图象与x轴相交于O、A两点, (1)、求这个二次函数的解析式(2)、在这条抛物线的对称轴右边的图象上有一点B,使△AOB的面积等于6.求点B的坐标。22. 如图,在 中,AB是直径,P为AB上一点,过点P作弦MN, °.
(1)、求这个二次函数的解析式(2)、在这条抛物线的对称轴右边的图象上有一点B,使△AOB的面积等于6.求点B的坐标。22. 如图,在 中,AB是直径,P为AB上一点,过点P作弦MN, °. (1)、若AP=2,BP=6,求MN的长.(2)、若MP=3 ;NP=5,求AB的长23. 如图,有长为30m的篱笆,一面利用墙(墙的最大可用长度为10m),围成中间隔有一道篱笆(平行于AB)的矩形花圃.设花圃的一边AB为xm,面积为ym2 .
(1)、若AP=2,BP=6,求MN的长.(2)、若MP=3 ;NP=5,求AB的长23. 如图,有长为30m的篱笆,一面利用墙(墙的最大可用长度为10m),围成中间隔有一道篱笆(平行于AB)的矩形花圃.设花圃的一边AB为xm,面积为ym2 . (1)、求y与x的函数关系式;(2)、如果要围成面积为63m2的花圃,AB的长是多少?(3)、能围成比63m2更大的花圃吗?如果能,请求出最大面积;如果不能,请说明理由.24. 如图,在直角坐标系中,点A的坐标为(-2,0),连结OA , 将线段OA绕原点O顺时针旋转120°,得到线段OB.
(1)、求y与x的函数关系式;(2)、如果要围成面积为63m2的花圃,AB的长是多少?(3)、能围成比63m2更大的花圃吗?如果能,请求出最大面积;如果不能,请说明理由.24. 如图,在直角坐标系中,点A的坐标为(-2,0),连结OA , 将线段OA绕原点O顺时针旋转120°,得到线段OB. (1)、求点B的坐标;(2)、求经过A、O、B三点的抛物线的解析式;(3)、在(2)中抛物线的对称轴上是否存在点C , 使△BOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由.(4)、如果点P是(2)中的抛物线上的动点,且在x轴的下方,那么△PAB是否有最大面积?若有,求出此时P点的坐标及△PAB的最大面积;若没有,请说明理由.
(1)、求点B的坐标;(2)、求经过A、O、B三点的抛物线的解析式;(3)、在(2)中抛物线的对称轴上是否存在点C , 使△BOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由.(4)、如果点P是(2)中的抛物线上的动点,且在x轴的下方,那么△PAB是否有最大面积?若有,求出此时P点的坐标及△PAB的最大面积;若没有,请说明理由.