四川省成都市成华区2019-2020学年九年级上学期数学期中试卷

试卷更新日期：2020-10-16 类型：期中考试

进入出卷网下载

一、单选题

1. 下列实数中，属于有理数的是（）

A、 $\sqrt{8}$ B、 $\frac{22}{7}$ C、 $\frac{π}{2}$ D、 $\sqrt[3]{2}$

查看试题解析
2. 不等式3x﹣5＜3+x的正整数解有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 下列判断中，错误的有（）
①0的绝对值是0；② $\frac{1}{3}$ 是无理数；③4的平方根是2；④1的倒数是-1．

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 下列四组数据中，“不能”作为直角三角形的三边长的是（）

A、3，4，6 B、5，12，13 C、6，8，10 D、 $\sqrt{2}$ ， $\sqrt{2}$ ，2

查看试题解析
5. 若 $\sqrt{x - 1}$ +（y+2）²＝0，则（x+y）²⁰²⁰等于（）

A、﹣1 B、1 C、3²⁰²⁰ D、﹣3²⁰²⁰

查看试题解析
6. 已知 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$ 是方程组 ${\begin{array}{l} a x + b y = 5 \\ b x + a y = 1 \end{array}$ 的解，则a+b的值是（）

A、﹣1 B、2 C、3 D、4

查看试题解析
7. 在平面直角坐标系中，若P（x﹣2，﹣x）在第三象限，则x的取值范围是（）

A、0＜x＜2 B、x＜2 C、x＞0 D、x＞2

查看试题解析
8. 已知点A（x，﹣4）与点B（3，y）关于x轴对称，那么x+y的值为（）

A、2 B、﹣1 C、7 D、1

查看试题解析
9. 如果最简二次根式 $\sqrt{3 a + 8}$ 与 $\sqrt{12 - a}$ 是同类二次根式，那么a的值为（）

A、1 B、±3 C、3 $\sqrt{2}$ D、3

查看试题解析
10. 一个长方形抽屉长12厘米，宽9厘米，贴抽屉底面放一根木棒，那么这根木棒最长（不计木棒粗细）可以是（）

A、15厘米 B、13厘米 C、9厘米 D、8厘米

查看试题解析

二、填空题

11. 如果二次根式 $\sqrt{3 - 2 x}$ 有意义，那么x的取值范围是．

查看试题解析
12. 已知x为整数，且满足 $- \sqrt{2} \leq x \leq \sqrt{3}$ ，则 $x =$ ．

查看试题解析
13. 直角三角形两直角边长分别为5和12，则它斜边上的高为．

查看试题解析
14. 如图，将长AB=5cm，宽AD=3cm的矩形纸片ABCD折叠，使点A与C重合，折痕为EF，则AE长为cm。

查看试题解析
15. 已知2a﹣1的平方根是±3，3a﹣b﹣1的立方根是2，a+b的平方根．

查看试题解析
16. 若方程（2m﹣6） $x^{| n | - 1}$ +（n+2） $y^{m^{2} - 8}$ ＝1是二元一次方程，则m＝， n＝．

查看试题解析
17. 已知：如图，等腰直角三角形ABC的直角边长为16，D在AB上，且DB＝4，M是在AC上的一动点，则DM+BM的最小值为．

查看试题解析
18. 已知关于x的不等式x﹣a≥0只有3个负整数解，则a的取值范围是．

查看试题解析
19. 如图，矩形ABOC中，A点的坐标为（－4，3），点D是BO边上一点，连接AD，把△ABD沿AD折叠，使点B落在点B′处．当△ODB′为直角三角形时，点D的坐标为．

查看试题解析
20. 如图，在等边△ABC中， M为BC边上的中点， D是射线AM上的一个动点，以CD为一边且在CD的下方作等边△CDE，连接BE．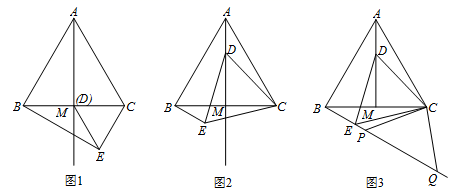

(1)、填空：若D与M重合时（如图1）∠CBE=度；

(2)、如图2，当点D在线段AM上时（点D不与A、M重合），请判断（1）中结论是否成立？并说明理由；

(3)、在（2）的条件下，如图3，若点P、Q在BE的延长线上，且CP=CQ=4，AB=6，试求PQ的长．

查看试题解析

三、解答题

21.

(1)、 ${(2020 - \sqrt{3})}^{0} + | 3 - \sqrt{12} | - \frac{6}{\sqrt{5}}$

(2)、 $(\sqrt{18} + \sqrt{12}) (3 \sqrt{2} - 2 \sqrt{3}) - {(\sqrt{3} - \sqrt{2})}^{2}$

查看试题解析
22. 解不等式（组）：

(1)、19﹣3（x+7）≤0

(2)、 ${\begin{array}{l} 2 (x + 3) - 4 > 3 x (1) \\ \frac{3 x + 2}{2} > x - 1 \end{array}$

查看试题解析
23. 解方程组： ${\begin{array}{l} 2 x - y = 7 \\ x + y = - 1 \end{array}$

查看试题解析
24. 如图，方格纸中每个小方格都是边长为1的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，A（﹣1，5），B（﹣1，0），C（﹣4，3）．

(1)、画出△ABC关于y轴成轴对称的△A₁B₁C₁；（其中A₁、B₁、C₁是A、B、C的对应点，不写画法）

(2)、写出A₁、B₁、C₁的坐标；

(3)、求出△A₁B₁C₁的面积．

查看试题解析
25. 已知： $a = \frac{1}{\sqrt{3} + 2}$ ， $b = \frac{1}{\sqrt{3} - 2}$ ，求代数式（a﹣3）（b﹣3）（a²+b²）的值．

查看试题解析
26. 把一堆花生分给一群猴子，如果每只猴子分3颗，就剩8颗；如果每只猴子分5颗，那么最后一只猴子分到的花生不足5颗。求猴子有多少只，花生有多少颗？（列不等式解答）

查看试题解析
27. 已知关于x、y的方程组 ${\begin{array}{l} x + y = 2 m + 7 \\ x - y = 4 m - 3 \end{array}$ 的解都为正数．

(1)、求m的取值范围；

(2)、化简：|3m+2|﹣|m﹣5|．

查看试题解析
28. 在Rt△ACB中，∠ACB＝90°，AC＝BC ， D为AB上一点，连结CD ，将CD绕C点逆时针旋转90°至CE ，连结DE ，过C作CF⊥DE交AB于F ，连结BE ．

(1)、求证：AD＝BE；

(2)、求证：AD²+BF²＝DF²；

(3)、若∠ACD＝15°，CD＝ $\sqrt{3}$ +1，求BF ．

查看试题解析
29. 在平面直角坐标系中，已知点O为坐标原点，点A（0，4）．△AOB是等边三角形，点B在第一象限．

(1)、如图①，求点B的坐标；

(2)、点P是x轴上的一个动点，连接AP，以点A为旋转中心，把△AOP逆时针旋转，使边AO与AB重合，得△ABD．
①如图②，当点P运动到点（ $\sqrt{3}$ ，0）时，求此时点D的坐标；

②求在点P运动过程中，使△OPD的面积等于 $\frac{\sqrt{3}}{4}$ 的点P的坐标（直接写出结果即可）．

查看试题解析