四川省巴中市恩阳区2019-2020学年九年级上学期数学期中试卷
试卷更新日期:2020-10-16 类型:期中考试
一、单选题
-
1. 下列运算正确的是( )A、 B、 C、 D、2. 二次根式 中 的取值范围是( )A、 B、 且 C、 D、 且3. 已知x=2是关于x的一元二次方程x2﹣x﹣2a=0的一个解,则a的值为( )A、0 B、﹣1 C、1 D、24. 如图,在 中, , , ,则 边的长等于( )
 A、6 B、8 C、10 D、125. 用配方法解一元二次方程x2﹣4x+2=0,下列配方正确的是( )A、(x+2)2=2 B、(x﹣2)2=﹣2 C、(x﹣2)2=2 D、(x﹣2)2=66. 如图, 是等边三角形,被一平行于 矩形所截, 被截成三等分,图中阴影部分的面积是 的面积的( )
A、6 B、8 C、10 D、125. 用配方法解一元二次方程x2﹣4x+2=0,下列配方正确的是( )A、(x+2)2=2 B、(x﹣2)2=﹣2 C、(x﹣2)2=2 D、(x﹣2)2=66. 如图, 是等边三角形,被一平行于 矩形所截, 被截成三等分,图中阴影部分的面积是 的面积的( )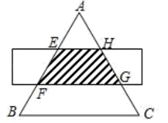 A、 B、 C、 D、7. 已知x,y是实数,且 +(y-3)2=0,则xy的值是( )A、4 B、-4 C、 D、-8. 如图,点D,E分别在△ABC的AB,AC边上,增加下列条件中的一个:①∠AED=∠B,②∠ADE=∠C,③ ,④ ,⑤AC2=AD•AE,使△ADE与△ACB一定相似的有( )
A、 B、 C、 D、7. 已知x,y是实数,且 +(y-3)2=0,则xy的值是( )A、4 B、-4 C、 D、-8. 如图,点D,E分别在△ABC的AB,AC边上,增加下列条件中的一个:①∠AED=∠B,②∠ADE=∠C,③ ,④ ,⑤AC2=AD•AE,使△ADE与△ACB一定相似的有( )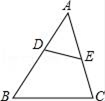 A、①②④ B、②④⑤ C、①②③④ D、①②③⑤9.
A、①②④ B、②④⑤ C、①②③④ D、①②③⑤9.如图,某小区计划在一块长为32m,宽为20m的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪,使草坪的面积为570m2 . 若设道路的宽为xm,则下面所列方程正确的是( )
 A、(32﹣2x)(20﹣x)=570 B、32x+2×20x=32×20﹣570 C、(32﹣x)(20﹣x)=32×20﹣570 D、32x+2×20x﹣2x2=57010. 如图,在直角△ABC中,∠BAC=90°,AB=3,M是边BC上的点,连接AM.如果将△ABM沿直线AM翻折后,点B恰好在边AC的中点处,那么点M到AC的距离是( )
A、(32﹣2x)(20﹣x)=570 B、32x+2×20x=32×20﹣570 C、(32﹣x)(20﹣x)=32×20﹣570 D、32x+2×20x﹣2x2=57010. 如图,在直角△ABC中,∠BAC=90°,AB=3,M是边BC上的点,连接AM.如果将△ABM沿直线AM翻折后,点B恰好在边AC的中点处,那么点M到AC的距离是( )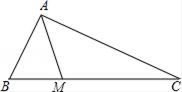 A、1.5 B、2 C、2.5 D、3
A、1.5 B、2 C、2.5 D、3二、填空题
-
11. 计算: =.12. 一元二次方程 化为一般形式为 .13. 如图,EF∥BC,若AE:EB=2:1,EM=1,MF=2.则BN:NC= .
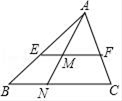 14. 三角形的每条边的长都是方程 的根,则三角形的周长是.15. 如图,在平面直角坐标系中,已知A(1,0),D(3,0),△ABC与△DEF位似,原点O是位似中心.若AB=1.5,则DE= .
14. 三角形的每条边的长都是方程 的根,则三角形的周长是.15. 如图,在平面直角坐标系中,已知A(1,0),D(3,0),△ABC与△DEF位似,原点O是位似中心.若AB=1.5,则DE= .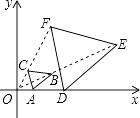
三、解答题
-
16. 计算:(1)、(2)、17. 解方程:(1)、(2)、18. 化简并求值:(1- )÷ ,其中x= -119. 若x,y都是实数,且y= +1,求 +3y的值.20. 已知关于x的方程x2+mx+m﹣3=0.(1)、若该方程的一个根为2,求m的值及方程的另一个根;(2)、求证:不论m取何实数,该方程都有两个不相等的实数根.21. 某商场销售一批名牌衬衫,平均每天可以销售20件,每件盈利40元,为了扩大销售,增加利润,尽量减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫降价1元,商场平均每天多售出2件,若商场平均每天要盈利1200元,每件衬衫应降价多少元?22. 已知:如图, .求证: .
 23. 如图,△ABC是一块锐角三角形材料,高线AH长8cm,底边BC长10cm,要把它加工成一个矩形零件,使矩形DEFG的一边EF在BC上,其余两个顶点D、G分别在AB、AC上,AH交DG于M.
23. 如图,△ABC是一块锐角三角形材料,高线AH长8cm,底边BC长10cm,要把它加工成一个矩形零件,使矩形DEFG的一边EF在BC上,其余两个顶点D、G分别在AB、AC上,AH交DG于M. (1)、求证:AM•BC=AH•DG;(2)、加工成的矩形零件DEFG的面积能否等于25cm2?若能,求出宽DE的长度;否则,请说明理由.24. 如图,有一块矩形硬纸板,长 ,宽 .在其四角各剪去一个同样的正方形,然后将四周突出部分折起,可制成一个无盖长方体盒子.当剪去正方形的边长取何值时,所得长方体盒子的侧面积为 ?
(1)、求证:AM•BC=AH•DG;(2)、加工成的矩形零件DEFG的面积能否等于25cm2?若能,求出宽DE的长度;否则,请说明理由.24. 如图,有一块矩形硬纸板,长 ,宽 .在其四角各剪去一个同样的正方形,然后将四周突出部分折起,可制成一个无盖长方体盒子.当剪去正方形的边长取何值时,所得长方体盒子的侧面积为 ?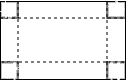 25. 如图,在 中. , , ,点 从点 开始沿 边向点 以 的速度移动,点 从点 开始沿 边向点 以 的速度移动.
25. 如图,在 中. , , ,点 从点 开始沿 边向点 以 的速度移动,点 从点 开始沿 边向点 以 的速度移动. (1)、如果点 、 分别从 、 同时出发,那么几秒后 的面积等于 ?(2)、在(1)中 的面积能否等于 ?请说明理由.26. 如图,四边形ABCD中,AD∥BC,AB=DC,AD=3cm,BC=7cm,∠B=60°,P为BC边上一点(不与B,C重合),连接AP,过P点作PE交DC于E,使得∠APE=∠B.
(1)、如果点 、 分别从 、 同时出发,那么几秒后 的面积等于 ?(2)、在(1)中 的面积能否等于 ?请说明理由.26. 如图,四边形ABCD中,AD∥BC,AB=DC,AD=3cm,BC=7cm,∠B=60°,P为BC边上一点(不与B,C重合),连接AP,过P点作PE交DC于E,使得∠APE=∠B. (1)、求证:△ABP∽△PCE;(2)、求AB的长;(3)、在边BC上是否存在一点P,使得DE:EC=5:3?如果存在,求BP的长;如果不存在,请说明理由.
(1)、求证:△ABP∽△PCE;(2)、求AB的长;(3)、在边BC上是否存在一点P,使得DE:EC=5:3?如果存在,求BP的长;如果不存在,请说明理由.