湖南省株洲市株洲县2019-2020学年九年级上学期数学期中试卷
试卷更新日期:2020-10-16 类型:期中考试
一、单选题
-
1. 下列函数关系式中属于反比例函数的是( )A、 B、 C、 D、2. 方程 的解是( )A、 B、 , C、 , D、3. 已知xy=mn,则把它改写成比例式后,错误的是( )A、 B、 C、 D、4. 已知m是方程x2﹣x﹣1=0的一个根,则代数式m2﹣m的值等于( )A、﹣1 B、0 C、1 D、25. 一元二次方程4x2+1=3x的根的情况是( )
A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根6. 若反比例函数 ,在每个象限内, 随 的增大而减小,则一次函数 的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 绿苑小区在规划设计时,准备在两幢楼房之间,设置一块面积为900平方米的矩形绿地,并且长比宽多10米.设绿地的宽为 米,根据题意,可列方程为( ).A、 B、 C、 D、8. 若关于x的一元二次方程 有实数根,则k的取值范围是( )A、k=4 B、k>4 C、k≤4且k≠0 D、k≤49. 如图,下列条件不能判定 的是.( ) A、 B、 C、 D、10. 如图,点 是反比例函数 的图象上任意一点, 轴交反比例函数 的图象于点 ,以 为边作平行四边形 ,其中 , 在 轴上,则 为( )
A、 B、 C、 D、10. 如图,点 是反比例函数 的图象上任意一点, 轴交反比例函数 的图象于点 ,以 为边作平行四边形 ,其中 , 在 轴上,则 为( )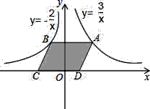 A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题
-
11. 已知 ,则 的值为.12. 已知 与 的函数表达式是 ,且 时, ,则 的值为 .13. 某校有两块相似的多边形草坪,其面积比为9:4,其中较大的一块草坪的周长是36米,则另一块草坪的周长是 .14. 若一个等腰三角形的三边长均满足方程x2-6x+8=0,则此三角形的周长为 .15. 把方程利用配方法 配成 的形式是 .16. 若 为一元二次方程 的两根,则代数式 的值为 .17. 如图,在△ABC中,D、E为边AB、AC的中点,已知△ADE的面积为4,那么△ABC的面积是 .
 18. 在平面直角坐标系中,直线y=﹣x+2与反比例函数y= 的图象有唯一公共点,若直线y=﹣x+b与反比例函数y= 的图象有2个公共点,则b的取值范围是 .
18. 在平面直角坐标系中,直线y=﹣x+2与反比例函数y= 的图象有唯一公共点,若直线y=﹣x+b与反比例函数y= 的图象有2个公共点,则b的取值范围是 .
三、解答题
-
19. 如图,为估算某河的宽度,在河对岸边选定一个目标点 ,在近岸取点 ,使得 ,点 在 上,并且点 在同一条直线上.若测得 米, 米, 米,试求河的宽度 .
 20. 先化简,再求值: ,其中 .21. 如图,已知一次函数 与反比例函数 的图象交于 两点,其中点 的坐标为(2,3).
20. 先化简,再求值: ,其中 .21. 如图,已知一次函数 与反比例函数 的图象交于 两点,其中点 的坐标为(2,3). (1)、求一次函数与反比例函数的解析式:(2)、请根据图象直接写出不等式 的解集.22. 已知关于 的方程 有两个实数根 , .(1)、求 的取值范围;(2)、若 ,求 的值.23.
(1)、求一次函数与反比例函数的解析式:(2)、请根据图象直接写出不等式 的解集.22. 已知关于 的方程 有两个实数根 , .(1)、求 的取值范围;(2)、若 ,求 的值.23.如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
 (1)、求证:△ABM∽△EFA;
(1)、求证:△ABM∽△EFA;
(2)、若AB=12,BM=5,求DE的长.24. 如图,已知函数 (x>0)的图象经过点A,B,点A的坐标为(1,2).过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC,OD. (1)、求△OCD的面积;
(1)、求△OCD的面积;
(2)、当BE= AC时,求CE的长.
25. 2017年,我市某楼盘以每平方米6500元的均价对外销售.因为楼盘滞销,房地产开发商为了加快资金周转,决定进行降价促销,经过连续两年平均下调10%后.(1)、求2019年我市楼盘以每平方米多少元的均价对外销售?(2)、假设2020年的均价仍然下调相同的百分率,张强准备购买一套100平方米的住房,他持有现金20万元,可以在银行贷款30万元,张强的愿望能否实现?(房价每平方米按照均价计算)26. 如图, 中, , , ,动点 从点 出发,在 边上以每秒 的速度向点 匀速运动,同时动点 从点 出发,在 边上以每秒 的速度向点 匀速运动,运动时间为 秒( ),连接 .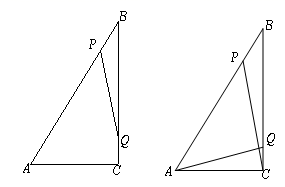 (1)、若 与 相似,求 的值;(2)、连接 , ,若 ,求 的值
(1)、若 与 相似,求 的值;(2)、连接 , ,若 ,求 的值