湖南省长沙市明德教育集团2019-2020学年九年级上学期数学期中试卷

试卷更新日期：2020-10-16 类型：期中考试

进入出卷网下载

一、单选题

1. 2018的相反数是（）

A、 $\frac{1}{2018}$ B、2018 C、-2018 D、 $- \frac{1}{2018}$

查看试题解析
2. 下列运算正确的是（）

A、 $a^{2} \cdot a^{5} = a^{10}$ B、 ${(3 a^{3})}^{2} = 6 a^{6}$ C、 ${(a + b)}^{2} = a^{2} + b^{2}$ D、 $(a + 2) (a - 3) = a^{2} - a - 6$

查看试题解析
3. 下列图形中，既是中心对称图形又是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
4. 已知 $⊙ O$ 的半径为 $5 c m$ ，若点 $A$ 到圆心 $O$ 的距离为 $3 c m$ ，则点 $A$ （）

A、在 $⊙ O$ 内 B、在 $⊙ O$ 上 C、在 $⊙ O$ 外 D、与 $⊙ O$ 的位置关系无法确定

查看试题解析
5. 国庆70周年大阅兵总编59个（方）梯队和联合军乐团，总规模约15000万人，是近几次阅兵中规模最大的一次，15000用科学记数法表示为（）

A、15×10³ B、1.5×10⁴ C、1.5×10⁵ D、0.15×10⁵

查看试题解析
6. 下列说法正确的是（）

A、调查湘江河水的水质情况，采用抽样调查的方式 B、数据2，0， $- 2$ ，1，3的中位数是 $- 2$ C、可能性是 $99 %$ 的事件在一次实验中一定会发生 D、从2000名学生中随机抽取100名学生进行调查，样本容量为2000名学生

查看试题解析
7. 如图所示， $⊙ O$ 的半径为13，弦的长度是24， $O N ⊥ A B$ ，垂足为 $N$ ，则 $O N =$ （）

A、5 B、7 C、9 D、11

查看试题解析
8. 已知函数 $y = \frac{k}{x}$ 的图象过点 $(2, - 3)$ ，则该函数的图象必在（）

A、第二、三象限 B、第二、四象限 C、第一、三象限 D、第三、四象限

查看试题解析
9. 如图，PA ， PB分别切⊙O于点A ， B ， OP交⊙O于点C ，连接AB ，下列结论中，错误的是（）

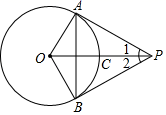A、∠1＝∠2 B、PA＝PB C、AB⊥OP D、OP＝2OA

查看试题解析
10. 如图，点B，C，D在⊙O上，若∠BCD＝130°，则∠BOD的度数是（）

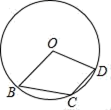A、50° B、60° C、80° D、100°

查看试题解析
11. 函数的图象 $y = (m + 1) x^{m^{2} - 2}$ 是双曲线，则m的值是（）

A、－1 B、0 C、1 D、2

查看试题解析
12. 如图，矩形ABCD中，AB=2， AD=2 $\sqrt{3}$ ，动点P从点A出发向终点D运动，连BP，并过点C作CH⊥BP，垂足为H.①△ABP∽△HCB；②AH的最小值为 $\sqrt{7}$ - $\sqrt{3}$ ； ③在运动过程中，BP扫过的面积始终等于CH扫过的面积：④在运动过程中，点H的运动路径的长为 $\frac{2}{3} \sqrt{3} π$ ，其中正确的有（）

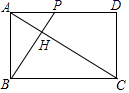A、①②③ B、①②④ C、②③④ D、①③④

查看试题解析

二、填空题

13. 九年级某同学6次数学小测验的成绩分别为：100，112，102，105，112，110，则该同学这6次成绩的众数是．

查看试题解析
14. 如图，在矩形 $A B C D$ 中， $E$ 是边 $A B$ 的中点，连接 $D E$ 交对角线 $A C$ 于点 $F$ ，若 $A B = 4$ ， $A D = 3$ ，则 $C F$ 的长为．

查看试题解析
15. 已知关于 $x$ 的一元二次方程 $x^{2} - k x - 6 = 0$ 的一个根为 $x ＝ 3$ ，则另一个根为．

查看试题解析
16. 使代数式 $\frac{\sqrt{x - 2}}{x - 3}$ 有意义的 $x$ 的取值范围是.

查看试题解析
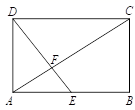17. 已知圆锥的底面半径为 $4 cm$ ，母线长为 $6 cm$ ，则它的侧面展开图的面积等于.

查看试题解析
18. 如图，已知双曲线 $y = \frac{k}{x} (x > 0)$ 经过矩形OABC边AB的中点F，交BC于点E，且四边形OEBF的面积为2，则k=.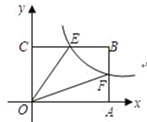

查看试题解析

三、解答题

19. 计算： ${(\sqrt{2} - π)}^{0} - | 1 - 2 \sqrt{3} | + \sqrt{12} - {(\frac{1}{2})}^{- 2}$ .

查看试题解析
20. 先化简，再求值： $(\frac{1}{x + 3} + \frac{6}{x^{2} - 9}) \div \frac{1}{x^{2} - 6 x + 9}$ ，其中 $x = \frac{1}{2}$ .

查看试题解析
21. 我国中小学生迎来了新版“教育部统编义务教育语文教科书”，本次“统编本”教材最引人关注的变化之一是强调对传统文化经典著作的阅读.某校对 $A$ 《三国演义》、 $B$ 《红楼梦》、 $C$ 《西游记》、 $D$ 《水浒》四大名著开展“最受欢迎的传统文化经典著作”调查，随机调查了若干名学生（每名学生必选且只能选这四大名著中的一部）并将得到的信息绘制了下面两幅不完整的统计图：

(1)、本次一共调查了名学生；

(2)、请将条形统计图补充完整；

(3)、某班语文老师想从这四大名著中随机选取两部作为学生暑期必读书籍，请用树状图或列表的方法求恰好选中《三国演义》和《红楼梦》的概率.

查看试题解析
22. 如图，已知一次函数 $y_{1} = k_{1} x + b (k_{1} \neq 0)$ 与反比例函数 $y_{2} = \frac{k_{2}}{x} (k_{2} \neq 0)$ 的图象交于 $A (4 ， 1)$ ， $B (n ， - 2)$ 两点.

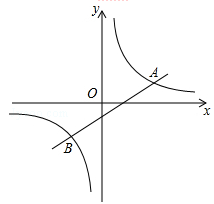(1)、求一次函数与反比例函数的解析式；

(2)、请根据图象直接写出 $y_{1} < y_{2}$ 时 $x$ 的取值范围.

查看试题解析
23. 今年义乌市准备争创全国卫生城市，某小区积极响应，决定在小区内安装垃圾分类的温馨提示牌和垃圾箱，若购买2个温馨提示牌和3个垃圾箱共需550元，且垃圾箱的单价是温馨提示牌单价的3倍.

(1)、求温馨提示牌和垃圾箱的单价各是多少元？

(2)、该小区至少需要安放48个垃圾箱，如果购买温馨提示牌和垃圾箱共100个，且费用不超过10000元，请你列举出所有购买方案，并指出哪种方案所需资金最少？最少是多少元？

查看试题解析
24. 如图， $A B$ 是 $⊙ O$ 的直径，点 $D$ 是弧 $A E$ 上一点，且 $∠ B D E = ∠ C B E$ ， $B D$ 与 $A E$ 交于点 $F$ ．

(1)、求证： $B C$ 是 $⊙ O$ 的切线；

(2)、若 $B D$ 平分 $∠ A B E$ ，求证： $D E^{2} = D F \cdot D B$ ；

(3)、在（2）的条件下，延长 $E D$ ， $B A$ 交于点 $P$ ，若 $P A = A O$ ， $D E = 2$ ，求 $P D$ 的长．

查看试题解析
25. 在平面直角坐标系 $x O y$ 中，点 $P$ 的坐标为 $(x_{1} ， y_{1})$ ，点 $Q$ 的坐标为 $(x_{2} ， y_{2})$ ，且 $x_{1} \neq x_{2}$ ， $y_{1} \neq y_{2}$ ，若 $P ， Q$ 为某个矩形的两个顶点，且该矩形的边均与某条坐标轴垂直，则称该矩形为点 $P ， Q$ 的“衍生矩形”．下图为点 $P ， Q$ 的“衍生矩形”的示意图．

(1)、已知点 $A$ 的坐标为 $(- 1 ， 0)$ ，点 $B$ 的坐标为 $(2 ， 4)$ 求点 $A ， B$ 的“衍生矩形”的面积；

(2)、已知点 $A$ 的坐标为 $(- 1 ， 0)$ ，点 $C$ 在直线 $x = 2$ 上，若点 $A ， C$ 的“衍生矩形”为正方形，求直线 $A C$ 的解析式；

(3)、 $⊙ O$ 的半径为 $\sqrt{2}$ ，点 $M$ 的坐标为 $(m ， 3)$ ．若在 $⊙ O$ 上存在一点 $N$ ，使得点 $M ， N$ 的“衍生矩形”为正方形，求 $m$ 的取值范围．

查看试题解析
26. 如图，已知二次函数y=ax²+bx+c（a≠0）的图象经过A（-1，0）、B（4，0）、C（0，2）三点．

(1)、求该二次函数的解析式；

(2)、点D是该二次函数图象上的一点，且满足∠DBA=∠CAO（O是坐标原点），求点D的坐标；

(3)、点P是该二次函数图象上位于一象限上的一动点，连接PA分别交BC，y轴与点E、F，若△PEB、△CEF的面积分别为S₁、S₂ ，求S₁-S₂的最大值．

查看试题解析