湖南省岳阳市汨罗市弼时片2019-2020学年九年级上学期数学期中试卷
试卷更新日期:2020-10-16 类型:期中考试
一、单选题
-
1. 若反比例函数y= 的图像经过点(﹣1,2),则这个函数的图象一定经过点( )A、(﹣2,﹣1) B、(﹣ ,2) C、(2,﹣1) D、( ,2)2. 已知反比例函数y=
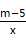 的图象在第二、四象限,则m的取值范围是( ) A、m≥5 B、m>5 C、m≤5 D、m<53. 方程 变为 的形式,正确的是( )A、 B、 C、 D、4. 甲、乙两同学解方程 ,甲看错了一次项,得根2和7,乙看错了常数项,得根1和 ,则原方程为( ).A、 B、 C、 D、5. 下列说法正确的是( )A、任意两个等腰三角形都相似 B、任意两个菱形都相似 C、任意两个正五边形都相似 D、对应角相等的两个多边形相似6. 如图,已知 ,那么下列结论正确的是( )
的图象在第二、四象限,则m的取值范围是( ) A、m≥5 B、m>5 C、m≤5 D、m<53. 方程 变为 的形式,正确的是( )A、 B、 C、 D、4. 甲、乙两同学解方程 ,甲看错了一次项,得根2和7,乙看错了常数项,得根1和 ,则原方程为( ).A、 B、 C、 D、5. 下列说法正确的是( )A、任意两个等腰三角形都相似 B、任意两个菱形都相似 C、任意两个正五边形都相似 D、对应角相等的两个多边形相似6. 如图,已知 ,那么下列结论正确的是( )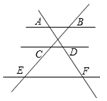 A、 B、 C、 D、7. 美是一种感觉,当人体下半身长与身高的比值越接近0.618时,越给人一种美感.某女模特身高165cm,下半身长x(cm)与身高l(cm)的比值是0.60.为尽可能达到好的效果,她应穿的高跟鞋的高度大约为( )A、4cm B、6cm C、8cm D、10cm8. 如图,反比例函数y=-
A、 B、 C、 D、7. 美是一种感觉,当人体下半身长与身高的比值越接近0.618时,越给人一种美感.某女模特身高165cm,下半身长x(cm)与身高l(cm)的比值是0.60.为尽可能达到好的效果,她应穿的高跟鞋的高度大约为( )A、4cm B、6cm C、8cm D、10cm8. 如图,反比例函数y=- 的图象与直线y=-
的图象与直线y=-  x的交点为A、B,过点A作y轴的平行线与过点B作的x轴的平行线相交于点C,则△ABC的面积为( )
x的交点为A、B,过点A作y轴的平行线与过点B作的x轴的平行线相交于点C,则△ABC的面积为( ) 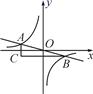 A、8 B、6 C、4 D、2
A、8 B、6 C、4 D、2二、填空题
-
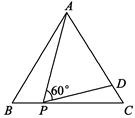
9. 若 ,则 .10. 三个顶点坐标分别为 ,以原点 为位似中心,将这个三角形放大为原来的2倍.相应坐标是(写出一种即可)11. 如图,等边△ABC的边长为3,点P为BC上一点,且BP=1,点D为AC上一点,若∠APD=60°,则CD的长为.
 12. 已知反比例函数 的图象经过点P(a+1,4),则a = .13. 某超市一月份的营业额为200万元,一月、二月、三月的营业额共1000万元,如果平均每月增长率为 ,则由题意列方程应为 。14. 某商品的进货价为每件 元,零售价为每件900元,为了适应市场竞争,商店按零售价的九折降低后再让利40元销售,仍可获利10%(相对于进价),则 元15. 老师给出了一个函数,甲、乙、丙三位学生分别指出了这个函数的一个性质,甲:第一象限内有它的图象;乙:第三象限内有它的图象;丙:在每个象限内, 随 的增大而减小. 请你写一个满足上述性质的函数解析式
12. 已知反比例函数 的图象经过点P(a+1,4),则a = .13. 某超市一月份的营业额为200万元,一月、二月、三月的营业额共1000万元,如果平均每月增长率为 ,则由题意列方程应为 。14. 某商品的进货价为每件 元,零售价为每件900元,为了适应市场竞争,商店按零售价的九折降低后再让利40元销售,仍可获利10%(相对于进价),则 元15. 老师给出了一个函数,甲、乙、丙三位学生分别指出了这个函数的一个性质,甲:第一象限内有它的图象;乙:第三象限内有它的图象;丙:在每个象限内, 随 的增大而减小. 请你写一个满足上述性质的函数解析式三、解答题
-
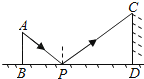
16. 如图是小明设计用手电来测量都匀南沙州古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经过平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是米(平面镜的厚度忽略不计).
 17. 解方程:(1)、 ;(2)、 .18. 关于 的一元二次方程 的一个根是1,求另一个根及 的值.19. 已知:关于x的方程(1)、当m取什么值时,原方程没有实数根;(2)、对m选取一个你喜欢的非零整数,使原方程有两个实数根,并求这两个实数根的平方和.20. 如图,已知四边形BDFE是菱形, ,且 ,求 的长度。
17. 解方程:(1)、 ;(2)、 .18. 关于 的一元二次方程 的一个根是1,求另一个根及 的值.19. 已知:关于x的方程(1)、当m取什么值时,原方程没有实数根;(2)、对m选取一个你喜欢的非零整数,使原方程有两个实数根,并求这两个实数根的平方和.20. 如图,已知四边形BDFE是菱形, ,且 ,求 的长度。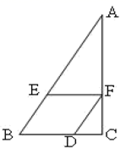 21. 某村计划在新农村改造过程中,拟筹资金2000元,计划在一块上、下底分别为10米、20米的梯形空地上种植花草(如图所示, ),村委会想在 地带与 地带种植单价为10元的太阳花,当 地带种满花后,已经花了500元,请你计算一下,若继续在 地带种植同样的太阳花,资金是否够用?并说明理由.
21. 某村计划在新农村改造过程中,拟筹资金2000元,计划在一块上、下底分别为10米、20米的梯形空地上种植花草(如图所示, ),村委会想在 地带与 地带种植单价为10元的太阳花,当 地带种满花后,已经花了500元,请你计算一下,若继续在 地带种植同样的太阳花,资金是否够用?并说明理由.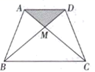 22. 为响应市委市政府提出的建设“绿色襄阳”的号召,我市某单位准备将院内一块长30m,宽20m的长方形空地,建成一个矩形花园.要求在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草,如图所示,要使种植花草的面积为532m2 , 那么小道进出口的宽度应为多少米?(注:所有小道进出口的宽度相等,且每段小道均为平行四边形)
22. 为响应市委市政府提出的建设“绿色襄阳”的号召,我市某单位准备将院内一块长30m,宽20m的长方形空地,建成一个矩形花园.要求在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草,如图所示,要使种植花草的面积为532m2 , 那么小道进出口的宽度应为多少米?(注:所有小道进出口的宽度相等,且每段小道均为平行四边形)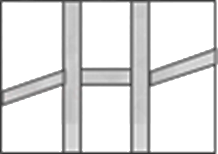 23. 如图,直线 与 轴交于点 ,与双曲线 交于点 ,其中点 在第一象限,点 在第三象限。
23. 如图,直线 与 轴交于点 ,与双曲线 交于点 ,其中点 在第一象限,点 在第三象限。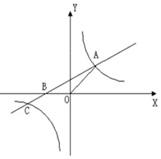 (1)、求双曲线的解析式;(2)、求 点的坐标;(3)、若 ,在 轴上是否存在点 ,使 是等腰三角形?若存在,请写出 点的坐标;若不存在,请说明理由。24. 如图,在矩形 中, 厘米, 厘米. 点 沿 边从 开始向点 以2厘米/秒的速度移动;点 沿 边从点 开始向点 以1厘米/秒速度移动.如果 、 同时出发,用 (秒)表示移动的时间 ,那么:
(1)、求双曲线的解析式;(2)、求 点的坐标;(3)、若 ,在 轴上是否存在点 ,使 是等腰三角形?若存在,请写出 点的坐标;若不存在,请说明理由。24. 如图,在矩形 中, 厘米, 厘米. 点 沿 边从 开始向点 以2厘米/秒的速度移动;点 沿 边从点 开始向点 以1厘米/秒速度移动.如果 、 同时出发,用 (秒)表示移动的时间 ,那么: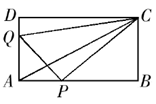 (1)、当 为何值时, 为等腰直角三角形?(2)、求四边形 的面积;提出一个与计算结果有关的结论;(3)、当 为何值时,以点 、 、 为顶点的三角形与 相似?
(1)、当 为何值时, 为等腰直角三角形?(2)、求四边形 的面积;提出一个与计算结果有关的结论;(3)、当 为何值时,以点 、 、 为顶点的三角形与 相似?