湖南省永州市新田县2019-2020学年九年级上学期数学期中试卷
试卷更新日期:2020-10-16 类型:期中考试
一、单选题
-
1. 下列函数中是反比例函数的是( )A、y=3x B、 C、 D、 (a为常数且a≠0)2. 已知四个非零实数a,b,c,d成比例,即 ,下列各式中不成立的是( )A、 B、 C、 D、3. 如图,已知直线 与双曲线 的一个交点坐标为(-1,3),则它们的另一个交点坐标是( )
 A、(1,3) B、(3,1) C、(1,-3) D、(-1,3)4. 对于函数 ,下列说法正确的是( )A、函数图象分别在第一、三象限 B、函数图象经过点(-1,2) C、当x>0时,y的值随x的值增大而减小 D、若点 , 在该反比例函数的图象上,则5. 将一元二次方程 配方后得到的结果是( )A、 B、 C、 D、6. 关于 的方程 有实数根,则k的取值范围是( )A、 B、 且 C、 D、 且7. 宽与长的比是 (约0.618)的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称的美感.我们可以用这样的方法画出黄金矩形:作正方形ABCD,分别取AD、BC的中点E、F,连接EF:以点F为圆心,以FD为半径画弧,交BC的延长线于点G;作GH⊥AD,交AD的延长线于点H,则图中下列矩形是黄金矩形的是( )
A、(1,3) B、(3,1) C、(1,-3) D、(-1,3)4. 对于函数 ,下列说法正确的是( )A、函数图象分别在第一、三象限 B、函数图象经过点(-1,2) C、当x>0时,y的值随x的值增大而减小 D、若点 , 在该反比例函数的图象上,则5. 将一元二次方程 配方后得到的结果是( )A、 B、 C、 D、6. 关于 的方程 有实数根,则k的取值范围是( )A、 B、 且 C、 D、 且7. 宽与长的比是 (约0.618)的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称的美感.我们可以用这样的方法画出黄金矩形:作正方形ABCD,分别取AD、BC的中点E、F,连接EF:以点F为圆心,以FD为半径画弧,交BC的延长线于点G;作GH⊥AD,交AD的延长线于点H,则图中下列矩形是黄金矩形的是( ) A、矩形ABFE B、矩形EFCD C、矩形EFGH D、矩形DCGH8. 如图,小正方形边长均为1,则下列图形中三角形(阴影部分)与△ABC相似的是( )
A、矩形ABFE B、矩形EFCD C、矩形EFGH D、矩形DCGH8. 如图,小正方形边长均为1,则下列图形中三角形(阴影部分)与△ABC相似的是( )
 A、
A、 B、
B、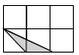 C、
C、 D、
D、 9. 在同一直角坐标系中,一次函数 与反比例函数 的图象大致是( )A、
9. 在同一直角坐标系中,一次函数 与反比例函数 的图象大致是( )A、 B、
B、 C、
C、 D、
D、 10. 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点 ,作正方形 ;延长 交x轴于点 ,作正方形 …按这样的规律进行下去,第2019个正方形的面积为( )
10. 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点 ,作正方形 ;延长 交x轴于点 ,作正方形 …按这样的规律进行下去,第2019个正方形的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 方程 的解为 .12. 如图,点A在某反比例函数的图象上,AC⊥ 轴,垂足为点C,且△AOC的面积为1,则函数的表达式为 .
 13. 已知AB∥CD,AD与BC相交于点O.若 = ,AD=10,则AO=.
13. 已知AB∥CD,AD与BC相交于点O.若 = ,AD=10,则AO=. 14. 若A(x1 , y1),B(x2 , y2),C(x3 , y3)都是反比例函数 的图象上的点,且 ,则 , , 由小到大的顺序是 .15. 若x1、x2是一元二次方程ax2+bx+c=0(a≠0)的两个根, 则x1+x2 =- ,x1x2 = ;已知m、n是方程x2+2x-1=0 的两个根,则m2n+mn2=.16. 某地2017年为做好“精准扶贫”,投入资金1280万元用于异地安置,并规划投入资金逐年增加,计划在2019年投入资金2880万元.设年平均增长率为 ,根据题意可列出方程为 .17. 如图,在▱ABCD中,E为CD上一点,连接AE,BD交于点F,S△DEF:S△ABF=4:25,则DE:EC= .
14. 若A(x1 , y1),B(x2 , y2),C(x3 , y3)都是反比例函数 的图象上的点,且 ,则 , , 由小到大的顺序是 .15. 若x1、x2是一元二次方程ax2+bx+c=0(a≠0)的两个根, 则x1+x2 =- ,x1x2 = ;已知m、n是方程x2+2x-1=0 的两个根,则m2n+mn2=.16. 某地2017年为做好“精准扶贫”,投入资金1280万元用于异地安置,并规划投入资金逐年增加,计划在2019年投入资金2880万元.设年平均增长率为 ,根据题意可列出方程为 .17. 如图,在▱ABCD中,E为CD上一点,连接AE,BD交于点F,S△DEF:S△ABF=4:25,则DE:EC= . 18. 如图,矩形OABC的边OA、OC分别在x轴、y轴上,点B 的坐标为(8,4),反比例函数y= (k>0)的图象分别交边BC、AB 于点D、E , 连结DE , △DEF与△DEB关于直线DE对称,当点F恰好落在线段OA上时,则k的值是.
18. 如图,矩形OABC的边OA、OC分别在x轴、y轴上,点B 的坐标为(8,4),反比例函数y= (k>0)的图象分别交边BC、AB 于点D、E , 连结DE , △DEF与△DEB关于直线DE对称,当点F恰好落在线段OA上时,则k的值是.
三、解答题
-
19. 解下列方程:(1)、(2)、20. 先化简,再求值: ,其中 满足 .21. 已知▱ABCD的两邻AB , AD的长是关于 的方程 的两个实数根.(1)、当m为何值时,▱ABCD是菱形?(2)、求出这时菱形的边长.22. 如图所示,已知AB⊥BD , ED⊥BD , AC⊥CE , 点B , D , C分别为垂足,点C是线段BD的中点,若ED=1,BD=4
 (1)、求证:△ABC∽△CDE .(2)、求AB的长.23. 一商店销售某种商品,平均每天可售出20件,每件盈利40元,为了扩大销售,增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.(1)、若降价a元,则平均每天销售数量为件.(用含a的代数式表示)(2)、当每件商品降价多少元时,该商店每天销售利润为1200元.24. 如图:一次函数 的图象与反比例函数 的图象交于M、N两点
(1)、求证:△ABC∽△CDE .(2)、求AB的长.23. 一商店销售某种商品,平均每天可售出20件,每件盈利40元,为了扩大销售,增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.(1)、若降价a元,则平均每天销售数量为件.(用含a的代数式表示)(2)、当每件商品降价多少元时,该商店每天销售利润为1200元.24. 如图:一次函数 的图象与反比例函数 的图象交于M、N两点 (1)、求反比例函数和一次函数的关系式(2)、根据图象写出使反比例函数的值大于一次函数的值的x的取值范围25. 定义:在平面直角坐标系中,把点先向右平移1个单位,再向上平移2个单位的平移称为一次斜平移.已知点A(1,0),点A经过n次斜平移得到点B,点M是线段AB的中点.
(1)、求反比例函数和一次函数的关系式(2)、根据图象写出使反比例函数的值大于一次函数的值的x的取值范围25. 定义:在平面直角坐标系中,把点先向右平移1个单位,再向上平移2个单位的平移称为一次斜平移.已知点A(1,0),点A经过n次斜平移得到点B,点M是线段AB的中点. (1)、当n=3时,点B的坐标是 , 点M的坐标是;(2)、如图1,当点M落在 的图像上,求n的值;(3)、如图2,当点M落在直线 上 , 点C是点B关于直线 的对称点,BC与直线 相交于点N.
(1)、当n=3时,点B的坐标是 , 点M的坐标是;(2)、如图1,当点M落在 的图像上,求n的值;(3)、如图2,当点M落在直线 上 , 点C是点B关于直线 的对称点,BC与直线 相交于点N.①求证:△ABC是直角三角形
②当点C的坐标为(5,3)时,求MN的长.
26. 类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整.原题:如图1,在平行四边形ABCD中,点E是BC的中点,点F是线段AE上一点,BF的延长线交射线CD于点G . 若 ,求 的值.
 (1)、尝试探究
(1)、尝试探究在图1中,过点E作EH∥AB交BG于点H , 则AB和EH的数量关系是 , CG和EH的数量关系是 , 的值是 .
(2)、类比延伸如图2,在原题的条件下,若 求 的值(用含有m的代数式表示).
(3)、拓展迁移如图3,梯形ABCD中,DC∥AB , 点E是BC的延长线上的一点,AE和BD相交于点F. 若 ,求 的值.