湖南省永州市蓝山县2019-2020学年九年级上学期数学期中试卷

试卷更新日期：2020-10-16 类型：期中考试

进入出卷网下载

一、单选题

1. 下列函数中，是反比例函数的为（　　）

A、y= $\frac{1}{5 x}$ B、y= $\frac{2}{x^{2}}$ C、y=2x+1 D、2y=x

查看试题解析
2. 关于反比例函数 $y = \frac{3}{x}$ 的图象，下列说法正确的是（）．

A、必经过点（2，1） B、两个分支分布在第二、四象限 C、两个分支关于y轴成轴对称 D、两个分支关于原点成中心对称

查看试题解析
3. 下列方程中，是一元二次方程的是（）

A、x²+2=yx² B、x²+5x=(x+3)(x-3) C、(x-1)²=5 D、 $\frac{1}{x^{2}} + \frac{1}{x} = 1$

查看试题解析
4. 已知正五边形ABCDE与正五边形 $A' B' C' D' E'$ 的面积比为1:2，则它们的相似比为（）

A、1:2 B、2:1 C、 $1 : \sqrt{2}$ D、 $\sqrt{2} : 1$

查看试题解析
5. 若方程 $(m - 2) x^{m^{2} - 2} + 2 x - 1 = 0$ 是关于 $x$ 的一元二次方程，则m的值是（）

A、2 B、-2 C、 $\pm 2$ D、3

查看试题解析
6. 若 $\frac{a}{2} = \frac{b}{3}$ ，则 $\frac{3 a - 2 b}{a + b}$ 的值是（）

A、 $\frac{7}{5}$ B、 $\frac{2}{3}$ C、 $\frac{12}{5}$ D、0

查看试题解析
7. 已知一元二次方程 $x^{2} - 6 x + c = 0$ 有一个根为2，则另一根为（）

A、2 B、3 C、4 D、8

查看试题解析
8. 如图，AB∥CD，AC，BD，EF相交于点O，则图中相似三角形共有（）

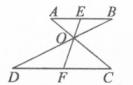A、1对 B、2对 C、3对 D、4对

查看试题解析
9. 如图，A、B两点在双曲线 $y = \frac{6}{x}$ 上，分别经过A、B两点向坐标轴作垂线段，已知 $S_{阴影} = 2$ ，则 $S_{1} + S_{2} =$ （）

A、 $4$ B、 $5$ C、 $6$ D、 $8$

查看试题解析
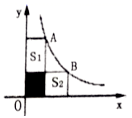10. 如图所示，不能判定△ABC∽△DAC的条件是（）

A、∠B＝∠DAC B、∠BAC＝∠ADC C、AC²＝DC·BC D、AD²＝BD·BC

查看试题解析

二、填空题

11. 如果四条线段m，n，x，y成比例，若m=2 ， n=8 ， y=4．则线段x的长是．

查看试题解析
12. 小颖测得2m高的标杆在太阳下的影长为1.2m，同时又测得一棵树的影长为2.4m，请你帮助小颖计算出这棵树的高度为m．

查看试题解析
13. 如果关于x的方程x²-2x+a-1=0有两个相等的实数根，那么a的值等于．

查看试题解析
14. 已知A(－1，y₁)，B(2，y₂)两点在双曲线 $y = \frac{k}{x}$ 上，且k＞0，则y₁y₂（填＞或＜）．

查看试题解析
15. 如图，一次函数y＝kx+b的图象与反比例函数 $y = \frac{m}{x}$ 的图象交于A（﹣2，1）、B（1，﹣2）两点．一次函数的值大于反比例函数的值时x的取值范围是．

查看试题解析
16. 方程 $x (x - 3) = x - 3$ 的解是.

查看试题解析
17. 若反比例函数， $y = \frac{k}{x}$ 的图象过点（-2，1）则一次函数y=kx-k的图象经过第象限．

查看试题解析
18. 把一矩形纸片对折，如果对折后的矩形与原矩形相似，则原矩形纸片的长与宽之比为

查看试题解析

三、解答题

19. 计算： $\sqrt{12} + 2014^{0} + | - 2 | \sin 60 ° - 4 \cos 30 °$

查看试题解析
20. 如图所示，在锐角△ABC中，AD，BE分别是边BC，AC上的高，
求证： $\frac{A D}{B E} = \frac{A C}{B C}$ ．

查看试题解析
21. 如图，直线y=2x-6与反比例函数 $y = \frac{k}{x}$ 的图象交于点A（4，2），与x轴交于点B．

(1)、求k的值及点B的坐标；

(2)、求△OAB的面积．

查看试题解析
22. 如图，利用一面墙（墙的长度不超过45m），用80m长的篱笆围一个矩形场地．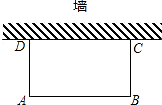

(1)、怎样围才能使矩形场地的面积为750m²？

(2)、能否使所围矩形场地的面积为810m² ，为什么？

查看试题解析
23. 已知，如图所示的双曲线是函数 $y = \frac{m - 3}{x}$ （m为常数，x＞0）图象的一支．

(1)、求常数m的取值范围；

(2)、若该函数的图象与一次函数y=x+1的图象在第一象限的交点为A（2，n），求点A的坐标及反比例函数的表达式．

查看试题解析
24. 如图，△ABC是等边三角形，点D、E分别在BC、AC上，且BD=CE ， AD与BE相交于点F ．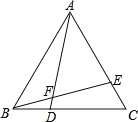

(1)、试说明△ABD≌△BCE；

(2)、△EAF与△EBA相似吗？说说你的理由．

查看试题解析
25. 在矩形ABCD中，AB＝5 cm，BC＝6 cm，点P从点A开始沿AB向终点B以1 cm/s的速度移动，与此同时，点Q从点B开始沿边BC向终点C以2 cm/s的速度移动，如果P、Q分别从A、B同时出发，当点Q运动到点C时，两点停止运动，设运动时间为t秒．

(1)、填空：BQ＝， PB＝(用含t的代数式表示)；

(2)、当t为何值时，PQ的长度等于 $2 \sqrt{10}$ cm?

(3)、是否存在t的值，使得五边形APQCD的面积等于26 cm²？若存在，请求出此时t的值；若不存在，请说明理由．

查看试题解析
26.
如图，已知矩形OABC中，OA=2，AB=4，双曲线 $y = \frac{k}{x}$ （k＞0）与矩形两边AB、BC分别交于E、F．

(1)、若E是AB的中点，求F点的坐标；

(2)、若将△BEF沿直线EF对折，B点落在x轴上的D点，作EG⊥OC，垂足为G，证明△EGD∽△DCF，并求k的值．

查看试题解析