湖南省娄底市2019-2020学年九年级上学期数学期中试卷

试卷更新日期：2020-10-16 类型：期中考试

进入出卷网下载

一、单选题

1. 已知反比例函数y= $\frac{k}{x}$ 的图象经过点（2，3），那么下列四个点中，也在这个函数图象上的是（）

A、（﹣6，1） B、（1，6） C、（2，﹣3） D、（3，﹣2）

查看试题解析
2. 方程 $(m - 3) x^{m^{2} - 7} - m x + 5 = 0$ 是关于 $x$ 的一元二次方程，则 $m$ 的值为（）

A、3 B、－3 C、±3 D、不存在

查看试题解析
3. 若反比例函数 $y = \frac{k}{x}$ 的图象分布在二、四象限，则关于x的方程 $k x^{2} - 3 x + 2 = 0$ 的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、只有一个实数根

查看试题解析
4. 如图，已知 $∠ D A B = ∠ C A E$ ，那么添加下列一个条件后，仍然无法判定 $△ A B C ∽ △ A D E$ 的是（）

A、 $\frac{A B}{A D} = \frac{B C}{D E}$ B、 $\frac{A B}{A D} = \frac{A C}{A E}$ C、 $∠ B = ∠ D$ D、 $∠ C = ∠ AED$

查看试题解析
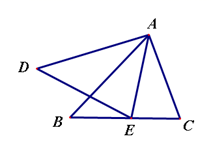5. 若2x-5y=0，且xy≠0,则 $\frac{x}{y} =$ （）

A、 $\frac{2}{5}$ B、 $- \frac{2}{5}$ C、 $\frac{5}{2}$ D、 $- \frac{5}{2}$

查看试题解析
6. 已知正比例函数 $y = - 4 x$ 与反比例函数 $y = \frac{k}{x}$ 的图象交于A、B两点，若点A（a,4），则点B的坐标为（）

A、（－1,4） B、（1,－4） C、（4，－1） D、（－4,1）

查看试题解析
7. 下列各组图形一定相似的是（）。

A、任意两个平行四边形 B、任意两个矩形 C、任意两个菱形 D、任意两个正方形

查看试题解析
8. 在函数 $y = \frac{1}{- 2 x}$ 的图象上有三点A₁（x₁ ， y₁）、A₂（x₂ ， y₂）、A₃（x₃ ， y₃），若x₁＜0＜x₂＜x₃ ，则下列正确的是（）

A、y₁＜0＜y₂＜y₃ B、y₂＜y₃＜0＜y₁ C、y₂＜y₃＜y₁＜0 D、0＜y₂＜y₁＜y₃

查看试题解析
9. 如图，在△ABC中，∠BAC=90°，F是BA延长线上一点， FD⊥BC于D，交AC于点E，则图中相似三角形共有几对（）

A、6对 B、5对 C、4对 D、3对

查看试题解析
10. 如图，在宽度为20m，长为32m的矩形地面上修筑同样宽的道路（图中阴影部分），余下的部分种上草坪，要使草坪的面积为540m² ，求道路的宽.如果设小路宽为xm，根据题意，所列方程正确的是（）

A、（20+x）（32﹣x）＝540 B、（20﹣x）（32﹣x）＝100 C、（20﹣x）（32﹣x）＝540 D、（20+x）（32﹣x）＝540

查看试题解析
11. 如图，平面直角坐标系中，点A是x轴负半轴上一个定点，点P是函数 $y = \frac{- 6}{x} (x < 0)$ 上一个动点， $P B ⊥ y$ 轴于点B ，当点P的横坐标逐渐增大时，四边形OAPB的面积将会 $($ $)$

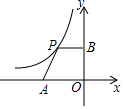A、先增后减 B、先减后增 C、逐渐减小 D、逐渐增大

查看试题解析

二、填空题

12. 把一元二次方程3x（x﹣2）=4化为一般形式是．

查看试题解析
13. 双曲线 $y = \frac{m - 2}{x}$ 在每个象限内，函数值y随x的增大而增大，则m的取值范围是

查看试题解析
14. 已知 $\frac{b}{a} = \frac{1}{3}$ ，则 $\frac{a - b}{a + b} =$

查看试题解析
15. 如图，△ABC中，DE∥BC交AB于点D，交AC于点E， BD=2，AB=6，AC=9，则AE的长为

查看试题解析
16. 若 $α$ ， $β$ 是一元二次方程 $x^{2} - 4 x + 2 = 0$ 的两根，则 $\frac{2}{α} + \frac{2}{β}$ 的值是。

查看试题解析
17. 若 $\frac{b + c}{a} = \frac{c + a}{b} = \frac{a + b}{c} = k$ ,则k的值为。

查看试题解析

三、解答题

18. 解下列方程:

(1)、 ${(2 x - 5)}^{2} = 2 (2 x - 5)$

(2)、 $3 x^{2} + 7 x + 2 = 0$

查看试题解析
19. 某校举行田径运动会，学校准备了某种气球，这些全球内充满了一定质量的气体，当温度不变时，气球内气体的气压p（kPa）是气体体积V（ $m^{3}$ ）的反比例函数，其图象如图所示：

(1)、求这个函数的表达式；

(2)、当气球内的气压大于150 kPa时，气球将会爆炸，为了安全起见，气体的体积应至少是多少？

查看试题解析
20. 矩形ABCD中，E为BC上一点，DF⊥AE于点F，AB＝6m，AD＝12m，CE＝4m.

(1)、求证：△ABE∽△DFA；

(2)、求AF的长.

查看试题解析
21. 如图，在平面直角坐标系xOy中，正比例函数 $y = - \frac{3}{2} x$ 与反比例函数 $y = \frac{k}{x}$ 的图象在第二象限交于点A ，且点A的横坐标为－2．

(1)、求反比例函数的解析式；

(2)、点B的坐标为(－4，0)，若点P在y轴上，且△AOP的面积与△AOB的面积相等，求出点P的坐标．

查看试题解析
22. 娄底市某楼盘准备以每平方米5000元的均价对外销售，由于国务院有关房地产的新政策出台后，购房者持币观望.为了加快资金周转，房地产开发商对价格经过两次下调后，决定以每平方米4050元的均价开盘销售.

(1)、求平均每次下调的百分率；

(2)、某人准备以开盘均价购买一套150平方米的房子.开发商还给予以下两种优惠方案以供选择：①打9.8折销售；②不打折，送三年物业管理费.物业管理费为每平方米每月1.5元.请问哪种方案更优惠？

查看试题解析
23. 如图，△ABC中， D、E是AB上的两点，△CDE是等边三角形.

求证：

(1)、△ABC∽△ACD；

(2)、△ACD∽△CBE；

(3)、 ${DE}^{2} = AD \cdot BF$ .

查看试题解析
24. 如图，Rt△ABC中，∠ACB=90°，AC=16，BC=4，D为AB上一点，DE⊥AC于点E，DE=1，P为CE上一动点，设CP的长为a.

(1)、求CE的长；

(2)、a为何值时，△DEP与△BCP相似？

(3)、当PD+PB有最小值时，求a的值及最小值.

查看试题解析
25. 已知反比例函数 $y = \frac{6}{x}$ 与一次函数 $y = kx + 5$ （k≠0），一次函数的图象与y轴交于点C，与x轴交于点D.

(1)、当k=－1时，如图，设直线 $y = kx + 5$ 与双曲线 $y = \frac{6}{x}$ 的两个交点为A、B（B在A的右边），求△OAB的面积；

(2)、若直线 $y = kx + 5$ 与双曲线 $y = \frac{6}{x}$ 总有两个不同的交点，求k的取值范围；

(3)、若直线 $y = kx + 5$ 与双曲线 $y = \frac{6}{x}$ 交于不同的两点M（ $x_{1} ， y_{1}$ ）、N（ $x_{2} ， y_{2}$ ），且满足 $| x_{1} - x_{2} | = 7$ ，求k的值.

查看试题解析