四川省简阳市简城学区2020-2021学年九年级上学期数学第一次月考试卷

试卷更新日期：2020-10-15 类型：月考试卷

进入出卷网下载

一、单选题

1. 已知关于x的一元二次方程 $x^{2} - x + k = 0$ 的一个根是2，则k的值是（）

A、-2 B、2 C、1 D、﹣1

查看试题解析
2. 下列图形中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 如图，在▱ABCD中，下列说法一定正确的是（）

A、AC＝BD B、AC⊥BD C、AB＝CD D、AB＝BC

查看试题解析
4. 如图，在菱形ABCD中，对角线AC、BD相交于点O，E为AB的中点，且OE=a，则菱形ABCD的周长为（）

A、16a B、12a C、8a D、4a

查看试题解析
5. 菱形的两条对角线把菱形分成全等的直角三角形的个数是（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 下列性质中,矩形具有而一般平行四边形不具有的是（）。

A、对边相等 B、对角相等 C、对角线相等 D、对边平行

查看试题解析
7. 下列各未知数的值是方程 $3 x^{2} + x - 2 = 0$ 的解的是（）

A、 $x = 1$ B、 $x = - 1$ C、 $x = 2$ D、 $x = - 2$

查看试题解析
8. 下列各式是一元二次方程的是（）

A、 $3 - 5 x^{2} = x$ B、 $\frac{3}{x} + x^{2} - 1 = 0$ C、 $a x^{2} + b x + c = 0$ D、 $4 x - 1 = 0$

查看试题解析
9. 把方程 $x^{2} - 10 x = - 3$ 左边化成含有 $x$ 的完全平方式，其中正确的是（）

A、 $x^{2} - 10 x + {(- 5)}^{2} = 28$ B、 $x^{2} - 10 x + {(- 5)}^{2} = 22$ C、 $x^{2} + 10 x + 5^{2} = 22$ D、 $x^{2} - 10 x + 5 = 2$

查看试题解析
10. 顺次连接矩形各边中点得到的四边形是（）

A、平行四边形 B、矩形 C、菱形 D、正方形

查看试题解析

二、填空题

11. 一元二次方程 $5 x^{2} - 8 x + 3 = 0$ 的一次项系数是，常数项是.

查看试题解析
12. 已知菱形ABCD的周长为20cm，O是两条对角线的交点，AC＝8cm，DB＝6cm，菱形的边长是cm，面积是cm² ．

查看试题解析
13. 若方程（m+2）x^|m|+3mx+1=0是关于x的一元二次方程，则m= ．

查看试题解析
14. 如图，△ABC中，∠ACB＝90°，D为AB中点，BC＝6，CD＝5，则AB＝， AC＝．

查看试题解析
15. 使分式 $\frac{x^{2} - 5 x - 6}{x + 1}$ 的值等于零的x是．

查看试题解析
16. 已知：一个菱形的边长为6，面积为28，则该菱形的两对角线的长度之和是．

查看试题解析
17. 如图，已知P是正方形ABCD对角线BD上一点，且BP＝BC ，则∠ACP度数是度．

查看试题解析
18. 如图，在矩形ABCD中，AD=5，AB=8，点E为射线DC上一个动点，把△ADE沿直线AE折叠，当点D的对应点F刚好落在线段AB的垂直平分线上时，则DE的长为．

查看试题解析
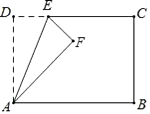19. 如图，在矩形ABCD中，AB＝3，AD＝4，以对角线的一半为边依次作平行四边形，则 $S_{平行四边形 O B B_{1} C}$ = ， $S_{平行四边形 O_{1} B_{1} B_{2} C_{1}}$ = .

查看试题解析

三、解答题

20. 解方程： ${(x - 3)}^{2} = 25$

查看试题解析
21. 用公式法解方程： $x^{2} - x - 1 = 0$ ．

查看试题解析
22. 用配方法解方程： $x^{2} - 6 x + 8 = 0$

查看试题解析
23. 矩形ABCD的对角线相交于点O．DE∥AC，CE∥BD．

(1)、求证：四边形OCED是菱形；

(2)、若∠ACB＝30°，菱形OCED的面积为 $8 \sqrt{3}$ ，求AC的长．

查看试题解析
24. 如图，点M，N分别是正方形ABCD的边BC，CD上的点，且BM＝CN， AM与BN交于点P，试探索AM与BN的关系.

(1)、数量关系，并证明；

(2)、位置关系，并证明.

查看试题解析
25. 如图，将矩形纸片ABCD沿对角线BD折叠，点C落在点E处，BE交AD于点F，连接AE.

求证：

(1)、BF＝DF；

(2)、AE∥BD；

(3)、若AB＝6，AD＝8，求BF的长.

查看试题解析
26. 将4个数a，b，c，d排成2行2列，两边各加一条竖线，记成 $| \begin{matrix} a & b \\ c & d \end{matrix} |$ ，定义 $| \begin{matrix} a & b \\ c & d \end{matrix} |$ ＝ad－bc，上述记法叫做二阶行列式．那么 $| \begin{matrix} x + 1 & x + 2 \\ x - 2 & 2 x \end{matrix} |$ ＝22表示的方程是一元二次方程吗？若是，请写出它的一般形式．

查看试题解析
27. 如图，已知E是平行四边形ABCD中BC边的中点，连接AE并延长AE交DC的延长线于点F。

(1)、求证：△ABE≌△FCE；

(2)、连接AC、BF，若AE＝ $\frac{1}{2}$ BC，求证：四边形ABFC为矩形；

(3)、在（2）条件下，当△ABC再满足一个什么条件时，四边形ABFC为正方形。

查看试题解析
28. 如图，在△ABC中，AB＝AC ， AD⊥BC于点D ， BC＝10cm ， AD＝8cm ， E点F点分别为AB ， AC的中点．

(1)、求证：四边形AEDF是菱形；

(2)、求菱形AEDF的面积；

(3)、若H从F点出发，在线段FE上以每秒2cm的速度向E点运动，点P从B点出发，在线段BC上以每秒3cm的速度向C点运动，问当t为何值时，四边形BPHE是平行四边形？当t取何值时，四边形PCFH是平行四边形？

查看试题解析