广西北师大平果附校2020-2021学年九年级上学期数学9月月考试卷
试卷更新日期:2020-10-15 类型:月考试卷
一、单选题
-
1. 下列函数是二次函数的是( )A、 B、 C、 D、2. 二次函数 的图象的顶点坐标是( )A、(1,3) B、(
 ,3)
C、(1,
,3)
C、(1,  )
D、(
)
D、(  ,
,  )
3. 二次函数 的最小值是 ( )A、 2 B、2 C、 1 D、14. 将抛物线 向上平移3个单位长度,再向右平移2个单位长度,所得到的抛物线为( ).A、 ; B、 ; C、 ; D、 .5. 二次函数 的图像大致为( )A、
)
3. 二次函数 的最小值是 ( )A、 2 B、2 C、 1 D、14. 将抛物线 向上平移3个单位长度,再向右平移2个单位长度,所得到的抛物线为( ).A、 ; B、 ; C、 ; D、 .5. 二次函数 的图像大致为( )A、 B、
B、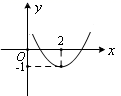 C、
C、 D、
D、 6. 抛物线y=(x﹣1)2﹣3的对称轴是( )
6. 抛物线y=(x﹣1)2﹣3的对称轴是( )
A、y轴 B、直线x=﹣1 C、直线x=1 D、直线x=﹣37. 抛物线y=x2+2x+m﹣1与x轴有两个不同的交点,则m的取值范围是( )A、m<2 B、m>2 C、0<m≤2 D、m<﹣28. 某公园有一个圆形喷水池,喷出的水流的高度h(单位:m)与水流运动时间t(单位:s)之间的关系式为 ,那么水流从喷出至回落到地面所需要的时间是( )
A、6s B、4s C、3s D、2s9. 二次函数y=x2﹣x﹣2的图象如图所示,则函数值y<0时x的取值范围是( ) A、x<﹣1 B、x>2 C、﹣1<x<2 D、x<﹣1或x>210. 在同一坐标系内,函数y=kx2和y=kx+2(k≠0)的图象大致如图( )A、
A、x<﹣1 B、x>2 C、﹣1<x<2 D、x<﹣1或x>210. 在同一坐标系内,函数y=kx2和y=kx+2(k≠0)的图象大致如图( )A、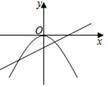 B、
B、 C、
C、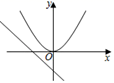 D、
D、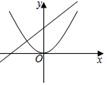 11.
11.已知二次函数的图象(0≤x≤3)如图所示,关于该函数在所给自变量取值范围内,下列说法正确的是( )
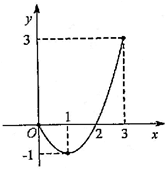 A、有最小值0,有最大值3 B、有最小值﹣1,有最大值0 C、有最小值﹣1,有最大值3 D、有最小值﹣1,无最大值12. 二次函数 ( )的图象如图所示,下列结论:① ;② ;③ ;④ ;⑤ ,其中正确的个数是( )
A、有最小值0,有最大值3 B、有最小值﹣1,有最大值0 C、有最小值﹣1,有最大值3 D、有最小值﹣1,无最大值12. 二次函数 ( )的图象如图所示,下列结论:① ;② ;③ ;④ ;⑤ ,其中正确的个数是( )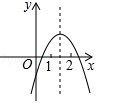 A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题
-
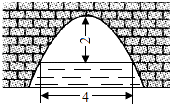
13. 函数 ,当k时,它的图像是开口向下的抛物线.14. 抛物线y=x2+2x+3与y轴的交点坐标为.15. 抛物线 是将抛物线 向平移个单位得到的.16. 已知抛物线 与 x轴只有一个公共点,则m= .17. 如图是一个横断面为抛物线形状的拱桥,当水面宽4米时,拱顶(拱桥洞的最高点)离水面2米,水面下降1米时,水面的宽度为米.
 18. 如果抛物线y=ax2-2ax+5与y轴交于点A,那么点A关于此抛物线对称轴的对称点坐标是.
18. 如果抛物线y=ax2-2ax+5与y轴交于点A,那么点A关于此抛物线对称轴的对称点坐标是.三、解答题
-
19. 已知二次函数 ,当 时, .(1)、当 时,求y的值;(2)、写出该函数图象的开口方向、对称轴和顶点坐标,并求当x为何值时,函数y随x的增大而增大.20. 已知函数y=3(x-4)2-27.(1)、写出此函数图象的开口方向、对称轴、顶点坐标;(2)、当x取何值时,y随x的增大而增大?x取何值时,y随x的增大而减小?(3)、当x取何值时,函数取得最值?并求出最值.21. 已知二次函数y=x2-2x-3.
 (1)、在平面直角坐标系中画出这个函数图象草图.(2)、结合图像回答:
(1)、在平面直角坐标系中画出这个函数图象草图.(2)、结合图像回答:①当 时,y有随着x的增大而 .
②不等式 的解集是 .
22. 已知二次函数的图象以 为顶点,且过点 .(1)、求该函数的关系式;(2)、求该函数图象与x轴的交点坐标.23. 某梁平特产专卖店销售“梁平柚”,已知“梁平柚”的进价为每个10元,现在的售价是每个16元,每天可卖出120个.市场调查反映:如调整价格,每涨价1元,每天要少卖出10个.设涨价x元,每天总获利y元.(1)、求y与x的函数关系式?(2)、请你帮专卖店老板算一算,涨价多少元时才能使利润最大,并求出此时的最大利润?24. 如图,已知抛物线y= +mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),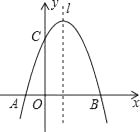 (1)、求m的值及抛物线的顶点坐标.(2)、点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.25. 居民小区要在一块一边靠墙(墙长 )的空地上修建一个矩形花园 ,花园的一边靠墙,另三边用总长为 的栅栏围成.如图,若设花园的一边为 ,花园的面积为 .
(1)、求m的值及抛物线的顶点坐标.(2)、点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.25. 居民小区要在一块一边靠墙(墙长 )的空地上修建一个矩形花园 ,花园的一边靠墙,另三边用总长为 的栅栏围成.如图,若设花园的一边为 ,花园的面积为 .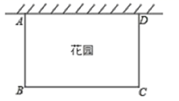 (1)、求y与x之间的数关系式,写出自变量x的取值范围;(2)、满足条件的花园面积能达到200 吗?如果能,求出此时的x的值;若不能,请说明理由;(3)、请结合题意判断:当x取何值时,花园的面积最大?最大面积为多少?26. 如图,在平面直角坐标系中,二次函数 (a>0)的图象与y轴交于点C,与x轴交于点A(﹣1,0)、B(3,0).
(1)、求y与x之间的数关系式,写出自变量x的取值范围;(2)、满足条件的花园面积能达到200 吗?如果能,求出此时的x的值;若不能,请说明理由;(3)、请结合题意判断:当x取何值时,花园的面积最大?最大面积为多少?26. 如图,在平面直角坐标系中,二次函数 (a>0)的图象与y轴交于点C,与x轴交于点A(﹣1,0)、B(3,0).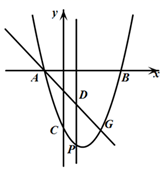 (1)、写出C点的坐标;(2)、求这个二次函数的解析式;(3)、若点G(2,y)是该抛物线上一点,点P是直线AG下方的抛物线上的一动点且PE垂直于x轴,交AG于D,当点P运动到什么位置时,线段PD的长最大?求此时点P的坐标和DP的最大值.
(1)、写出C点的坐标;(2)、求这个二次函数的解析式;(3)、若点G(2,y)是该抛物线上一点,点P是直线AG下方的抛物线上的一动点且PE垂直于x轴,交AG于D,当点P运动到什么位置时,线段PD的长最大?求此时点P的坐标和DP的最大值.