广东省揭阳市惠来县2020-2021学年九年级上学期数学第一次月考试卷

试卷更新日期：2020-10-15 类型：月考试卷

进入出卷网下载

一、单选题

1. 某班从甲、乙、丙、丁四位选中随机选取两人参加校乒乓球比赛，恰好选中甲、乙两位选手的概率是（）

A、 $\frac{1}{3}$ B、 $\frac{1}{4}$ C、 $\frac{1}{6}$ D、 $\frac{1}{8}$

查看试题解析
2. 一个口袋中有3个黑球和若干个白球，在不允许将球倒出来数的前提下，小明为估计其中的白球数，采用了如下的方法：从口袋中随机摸出一球，记下颜色，然后把它放回口袋中，摇匀后再随机摸出一球，记下颜色……不断重复，上述过程小明共摸了100次，其中20次摸到黑球．根据上述数据，小明可估计口袋中的白球大约有（）．

A、10个 B、12个 C、15个 D、18个

查看试题解析
3. 下列说法正确的是（）

A、一组对边平行另一组对边相等的四边形是平行四边形 B、对角线互相垂直平分的四边形是菱形 C、对角线相等的四边形是矩形 D、对角线互相垂直且相等的四边形是正方形

查看试题解析
4. 如图，在菱形 $A B C D$ 中，P是对角线 $A C$ 上一动点，过点P作 $P E ⊥ B C$ 于点E. $P F ⊥ A B$ 于点F.若菱形 $A B C D$ 的周长为20，面积为24，则 $P E + P F$ 的值为（）

A、4 B、 $\frac{24}{5}$ C、6 D、 $\frac{48}{5}$

查看试题解析
5. 已知关于x的一元二次方程x²+5x﹣m＝0的一个根是2，则另一个根是（）

A、﹣7 B、7 C、3 D、﹣3

查看试题解析
6. 如图，在长为 $62$ 米、宽为 $42$ 米的矩形草地上修同样宽的路，余下部分种植草坪，要使草坪的面积为 $2400$ 平方米，设道路的宽为x米．则可列方程为（）

A、 $(62 - x) (42 - x) = 2400$ B、 $(62 - x) (42 - x) + x^{2} = 2400$ C、 $62 \times 42 - 62 x - 42 x = 2400$ D、 $62 x + 42 x = 2400$

查看试题解析

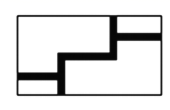7. 新冠疫情发生以来，为保证防控期间的口罩供应，某公司加紧转产，开设多条生产线争分夺秒赶制口罩，从最初转产时的陌生，到正式投产后达成日均生产100万个口罩的产能．不仅效率高，而且口罩送检合格率也不断提升，真正体现了“大国速度”．以下是质监局对一批口罩进行质量抽检的相关数据，统计如下：

抽检数量n/个	20	50	100	200	500	1000	2000	5000	10000
合格数量m/个	19	46	93	185	459	922	1840	4595	9213
口罩合格率 $\frac{m}{n}$	0.950	0.920	0.930	0.925	0.918	0.922	0.920	0.919	0.921

下面四个推断合理的是（）

A、当抽检口罩的数量是10000个时，口罩合格的数量是9213个，所以这批口罩中“口罩合格”的概率是0.921； B、由于抽检口罩的数量分别是50和2000个时，口罩合格率均是0.920，所以可以估计这批口罩中“口罩合格”的概率是0.920； C、随着抽检数量的增加，“口罩合格”的频率总在0.920附近摆动，显示出一定的稳定性，所以可以估计这批口罩中“口罩合格”的概率是0.920； D、当抽检口罩的数量达到20000个时，“口罩合格”的概率一定是0.921．

查看试题解析

8. 如图，对折矩形纸片ABCD，使AD与BC重合，得到折痕EF；把纸片展平后再次折叠，使点A落在EF上的点 $A^{'}$ 处，得到折痕BM，BM与FF相交于点N．若直线B A^’交直线CD于点O，BC＝5，EN＝1，则OD的长为（）

A、 $\frac{1}{2} \sqrt{3}$ B、 $\frac{1}{3} \sqrt{3}$ C、 $\frac{1}{4} \sqrt{3}$ D、 $\frac{1}{5} \sqrt{3}$

查看试题解析
9. 已知x₁、x₂是关于x的方程x²+mx﹣1＝0的两根，下列结论一定正确的是（）

A、x₁≠x₂ B、x₁+x₂＜0 C、x₁•x₂＞0 D、x₁＞0，x₂＜0

查看试题解析
10. 如图，四边形OAA₁B₁是边长为1的正方形，以对角线OA₁为边作第二个正方形OA₁A₂B₂ ，连接AA₂ ，得到 $△$ AA₁A₂；再以对角线OA₂为边作第三个正方形OA₂A₃B₃ ，连接A₁A₃ ，得到 $△$ A₁A₂A₃ ，再以对角线OA₃为边作第四个正方形OA₂A₄B₄ ，连接A₂A₄ ，得到 $△$ A₂A₃A₄ ， …，设 $△$ AA₁A₂ ， $△$ A₁A₂A₃ ， $△$ A₂A₃A₄ ， …，的面积分别为S₁ ， S₂ ， S₃ ， …，如此下去，则S₂₀₂₀的值为（）

A、 $\frac{1}{2^{2020}}$ B、2²⁰¹⁸ C、2²⁰¹⁸+ $\frac{1}{2}$ D、1010

查看试题解析

二、填空题

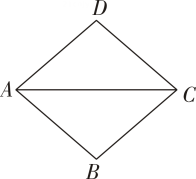
11. 盒子里有3张形状、大小、质地完全相同的卡片，上面分别标着数字1，2，3，从中随机抽出1张后不放回，再随机抽出1张，则两次抽出的卡片上的数字之和为奇数的概率是.

查看试题解析
12. 若x₁ ， x₂是方程x²﹣4x﹣2020＝0的两个实数根，则代数式x₁²﹣2x₁+2x₂的值等于.

查看试题解析
13. 如图，菱形ABCD中，∠ACD=40°，则∠ABC=°。

查看试题解析
14. 如图，已知AB⊥BC，AB=12cm，BC=8cm.一动点N从C点出发沿CB方向以1cm/s的速度向B点运动，同时另一动点M由点A沿AB方向以2cm/s的速度也向B点运动，其中一点到达B点时另一点也随之停止，当△MNB的面积为24cm²时运动的时间t为秒.

查看试题解析
15. 已知菱形 $A B C D$ 的一条对角线的长为 $4$ ，边 $A B$ 的长是 $x^{2} - 5 x + 6 = 0$ 的一个根，则菱形 $A B C D$ 的周长为．

查看试题解析
16. 如图，在矩形 $A B C D$ 中， $A D = 4 ， A B = 8$ ．分别以点 $B ， D$ 为圆心，以大于 $\frac{1}{2} B D$ 的长为半径画弧，两弧相交于点 $E$ 和 $F$ ．作直线 $E F$ 分别与 $D C ， D B ， A B$ 交于点 $M ， O ， N$ ，则 $M N =$ ．

查看试题解析
17. 如图，在边长为4的正方形 $A B C D$ 中将 $Δ A B D$ 沿射线 $B D$ 平移，得到 $Δ E G F$ ，连接 $E C$ 、 $G C$ ．求 $E C + G C$ 的最小值为．

查看试题解析

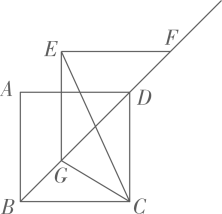
三、解答题

18. 解一元二次方程：

(1)、x²＋2x－1＝0；

(2)、(x－3)²＝2x－6.

查看试题解析
19. 随着“新冠肺炎”疫情防控形势日渐好转，各地开始复工复学，某校复学后成立“防疫志愿者服务队”，设立四个“服务监督岗”：①洗手监督岗，②戴口罩监督岗，③就餐监督岗，④操场活动监督岗.李老师和王老师报名参加了志愿者服务工作，学校将报名的志愿者随机分配到四个监督岗.

(1)、李老师被分配到“洗手监督岗”的概率为

(2)、用列表法或面树状图法，求李老师和王老师被分配到同一个监督岗的概率.

查看试题解析
20. 如图，在四边形 $A B C D$ 中， $A D // B C$ ，对角线 $B D$ 的垂直平分线与边 $A D$ 、 $B C$ 分别相交于M、N.

(1)、求证：四边形 $B N D M$ 是菱形；

(2)、若 $B D = 24$ ， $M N = 10$ ，求菱形 $B N D M$ 的周长.

查看试题解析
21. 某口罩生产厂生产的口罩1月份平均日产量为20000，1月底因突然爆发新冠肺炎疫情，市场对口罩需求量大增，为满足市场需求，工厂决定从2月份起扩大产能，3月份平均日产量达到24200个．

(1)、求口罩日产量的月平均增长率；

(2)、按照这个增长率，预计4月份平均日产量为多少？

查看试题解析
22. 中华文化源远流长，文学方面，《西游记》、《三国演义》、《水浒传》、《红楼梦》是我国古代长篇小说中的典型代表，被称为“四大古典名著”．某中学为了了解学生对四大古典名著的阅读情况，就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查，根据调查结果绘制成如下尚不完整的统计图．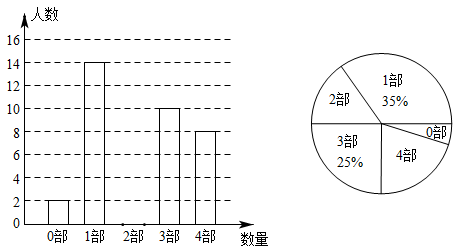

请根据以上信息，解决下列问题：

(1)、本次调查所得数据的众数是部，中位数是部；

(2)、扇形统计图中“4部”所在扇形的圆心角为度；

(3)、请将条形统计图补充完整；

(4)、没有读过四大古典名著的两名学生准备从中各自随机选择一部来阅读，请用列表或画树状图的方法求他们恰好选中同一名著的概率．

查看试题解析
23. 在全国人民的共同努力下，新冠疫情防控得到有效控制，复工复产后，某玩具经销商在销售中发现：某款进价为每个30元的玩具，若以每个40元销售，一个月能售出400个，销售单价每涨1元，月销售量就减少10个，请回答以下问题：

(1)、若上涨a元，则销量为个。

(2)、若月销售利润定为6000元，且尽可能让利消费者，销售单价应定为多少元？

(3)、由于资金问题，月销售成本不超过9000元(没有库存积压)，销售单价至少定为多少元？

查看试题解析
24. 等腰△ABC的直角边AB=BC=10cm，点P、Q分别从A、C两点同时出发，均以1cm/秒的相同速度作直线运动，已知P沿射线AB运动，Q沿边BC的延长线运动，PQ与直线AC相交于点D.设P点运动时间为t，△PCQ的面积为S.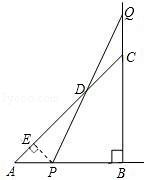

(1)、求出S关于t的函数关系式；

(2)、当点P运动几秒时，S_△_PCQ=S_△_ABC？

(3)、作PE⊥AC于点E，当点P、Q运动时，线段DE的长度是否改变？证明你的结论.

查看试题解析
25. 如图，∠MON＝90°，正方形ABCD的顶点A、B分别在OM、ON上，AB＝13，OB＝5，E为AC上一点，且∠EBC＝∠CBN，直线DE与ON交于点F.

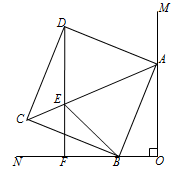(1)、求证BE＝DE；

(2)、判断DF与ON的位置关系，并说明理由；

(3)、△BEF的周长为.

查看试题解析