广东省佛山市顺德区三校2020-2021学年九年级上学期数学第一次月考试卷
试卷更新日期:2020-10-15 类型:月考试卷
一、单选题
-
1. 已知 ,则 的值为( )A、 B、 C、 D、2. 如图,AD∥BE∥CF,点B,E分别在AC,DF上,DE=2,EF=AB=3,则BC长为( )
 A、 B、2 C、 D、43. 某服装厂对一批服装进行质量抽检结果如下:
A、 B、2 C、 D、43. 某服装厂对一批服装进行质量抽检结果如下:抽取的服装数量
优等品数量
优等品的频率
则这批服装中,随机抽取一件是优等品的概率约为( )
A、 B、 C、 D、4. 已知一元二次方程 的较小根为x1 , 则下面对x1的估计正确的是A、 B、 C、 D、5. 平行四边形、矩形、菱形、正方形共有的性质是( )A、对角线相等 B、对角线互相垂直 C、对角线互相平分 D、对角形互相垂直平分6. 如图,△ABC与△DEF形状完全相同,且AB=3.6,BC=6,AC=8,EF=2,则DE的长度为( )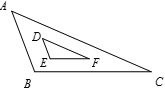 A、1.2 B、1.8 C、3 D、7.27. 如图,四边形 和四边形 是以点 为位似中心的位似图形,若 ,四边形 的面积等于4,则四边形 的面积为( )
A、1.2 B、1.8 C、3 D、7.27. 如图,四边形 和四边形 是以点 为位似中心的位似图形,若 ,四边形 的面积等于4,则四边形 的面积为( ) A、3 B、4 C、6 D、98. 若关于x的一元二次方程 有两个不相等的实数根,则实数k的取值范围是( )A、 B、 且 C、 D、 且9. 如图,矩形 的对角线 , 交于点 , , ,过点 作 ,交 于点 ,过点 作 ,垂足为 ,则 的值为( )
A、3 B、4 C、6 D、98. 若关于x的一元二次方程 有两个不相等的实数根,则实数k的取值范围是( )A、 B、 且 C、 D、 且9. 如图,矩形 的对角线 , 交于点 , , ,过点 作 ,交 于点 ,过点 作 ,垂足为 ,则 的值为( ) A、 B、 C、 D、10. 如图,在正方形 中,点P是 上一动点(不与 重合) ,对角线 相交于点O,过点P分别作 的垂线,分别交 于点 交 于点 .下列结论:① ;② ;③ ;④ ;⑤点O在 两点的连线上.其中正确的是( )
A、 B、 C、 D、10. 如图,在正方形 中,点P是 上一动点(不与 重合) ,对角线 相交于点O,过点P分别作 的垂线,分别交 于点 交 于点 .下列结论:① ;② ;③ ;④ ;⑤点O在 两点的连线上.其中正确的是( )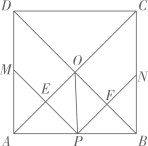 A、①②③④ B、①②③⑤ C、①②③④⑤ D、③④⑤
A、①②③④ B、①②③⑤ C、①②③④⑤ D、③④⑤二、填空题
-
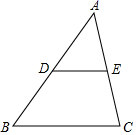
11. 如图,在 中,D,E分别是边 , 的中点.若 的面积为 .则四边形 的面积为 .
 12. 若从-2,0,1这三个数中任取两个数,其中一个记为a,另一个记为b,则点A(a, b)恰好落在x轴上的概率是。13. 在平面直角坐标系中, 和 的相似比等于 ,并且是关于原点O的位似图形,若点A的坐标为 ,则其对应点 的坐标是 .14. 有一人患流感,经过两轮传染后共有81人患了流感,则每轮传染中平均一人传染了人.15. 如图,折叠矩形纸片 ,使点D落在 边的点M处, 为折痕, , .设 的长为t,用含有t的式子表示四边形 的面积是.
12. 若从-2,0,1这三个数中任取两个数,其中一个记为a,另一个记为b,则点A(a, b)恰好落在x轴上的概率是。13. 在平面直角坐标系中, 和 的相似比等于 ,并且是关于原点O的位似图形,若点A的坐标为 ,则其对应点 的坐标是 .14. 有一人患流感,经过两轮传染后共有81人患了流感,则每轮传染中平均一人传染了人.15. 如图,折叠矩形纸片 ,使点D落在 边的点M处, 为折痕, , .设 的长为t,用含有t的式子表示四边形 的面积是. 16. 如图,等腰 中, ,边 的垂直平分线交 于点D,交 于点E.若 的周长为 ,则 的长为 .
16. 如图,等腰 中, ,边 的垂直平分线交 于点D,交 于点E.若 的周长为 ,则 的长为 .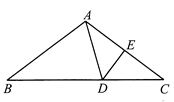 17. 如图,在正方形 中, 与 交于点 是 的中点,点 在 边上,且 为对角线 上一点, 则 的最大值为 .
17. 如图,在正方形 中, 与 交于点 是 的中点,点 在 边上,且 为对角线 上一点, 则 的最大值为 .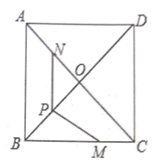
三、解答题
-
18. 解下列方程:(1)、(2)、19. 有3个完全相同的小球,把它们分别标号为1,2,3,放在一个不透明的口袋中,从口袋中随机摸出一个小球,记下标号后放回,再从口袋中随机摸出一个小球,记下标号.用画树状图(或列表)的方法,求两次摸出的小球号码恰好都大于1的概率.20. 已知 .(1)、求 的值;(2)、若 ,求x、y、z.21. 如图, 中, , ,分别在边 、 上的点E与点F关于 对称,连接 、 、 、 .
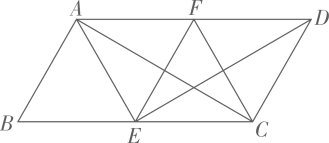 (1)、试判定四边形 的形状,并说明理由;(2)、求证:22. 某水果商场经销一种高档水果,原价每千克50元,连续两次降价后每千克32元,若每每次下降的百分率相同.(1)、求每次下降的百分率;(2)、若每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,商场决定采取适当的涨价措施,若每千克涨价1元,日销售量将减少20千克,现该商场要保证每天盈利6000元,且要尽快减少库存,那么每千克应涨价多少元?23. 广元市某中学举行了“禁毒知识竞赛”,王老师将九年级(1)班学生成绩划分为A、B、C、D、E五个等级,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题:
(1)、试判定四边形 的形状,并说明理由;(2)、求证:22. 某水果商场经销一种高档水果,原价每千克50元,连续两次降价后每千克32元,若每每次下降的百分率相同.(1)、求每次下降的百分率;(2)、若每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,商场决定采取适当的涨价措施,若每千克涨价1元,日销售量将减少20千克,现该商场要保证每天盈利6000元,且要尽快减少库存,那么每千克应涨价多少元?23. 广元市某中学举行了“禁毒知识竞赛”,王老师将九年级(1)班学生成绩划分为A、B、C、D、E五个等级,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题: (1)、求九年级(1)班共有多少名同学?(2)、补全条形统计图,并计算扇形统计图中的“C”所对应的圆心角度数;(3)、成绩为A类的5名同学中,有2名男生和3名女生;王老师想从这5名同学中任选2名同学进行交流,请用列表法或画树状图的方法求选取的2名同学都是女生的概率.24. 如图,在矩形ABCD中,AB=4,BC=3,点P,Q在对角线BD上,且BQ= BP,过点P作PH⊥AB于点H,连接HQ,以PH、HQ为邻边作平行四边形PHQG,设BQ=m.
(1)、求九年级(1)班共有多少名同学?(2)、补全条形统计图,并计算扇形统计图中的“C”所对应的圆心角度数;(3)、成绩为A类的5名同学中,有2名男生和3名女生;王老师想从这5名同学中任选2名同学进行交流,请用列表法或画树状图的方法求选取的2名同学都是女生的概率.24. 如图,在矩形ABCD中,AB=4,BC=3,点P,Q在对角线BD上,且BQ= BP,过点P作PH⊥AB于点H,连接HQ,以PH、HQ为邻边作平行四边形PHQG,设BQ=m.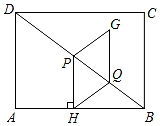 (1)、若m=2时,求此时PH的长.(2)、若点C,G,H在同一直线上时,求此时的m值.(3)、若经过点G的直线将矩形ABCD的面积平分,同时该直线将平行四边形PHQG的面积分成1:3的两部分,求此时m的值.25. 如图,已知△ABC中,AC=BC,∠ACB=120°,P为△ABC内部一点,且满足∠APB=∠BPC=150°.
(1)、若m=2时,求此时PH的长.(2)、若点C,G,H在同一直线上时,求此时的m值.(3)、若经过点G的直线将矩形ABCD的面积平分,同时该直线将平行四边形PHQG的面积分成1:3的两部分,求此时m的值.25. 如图,已知△ABC中,AC=BC,∠ACB=120°,P为△ABC内部一点,且满足∠APB=∠BPC=150°.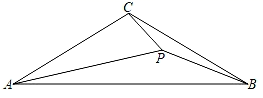 (1)、求证:△PAB∽△PBC;(2)、求证:PA=3PC;(3)、若AB=10,求PA的长.
(1)、求证:△PAB∽△PBC;(2)、求证:PA=3PC;(3)、若AB=10,求PA的长.