安徽合肥市包河四十八分校2020-2021学年九年级上学期数学第一次月考试卷
试卷更新日期:2020-10-15 类型:月考试卷
一、单选题
-
1. 下列函数是二次函数的是( )A、y=2x2-3 B、y=ax2 C、y=2(x+3)2-2x2 D、2. 函数y=﹣x2﹣4x﹣3图象顶点坐标是( )A、(2,﹣1) B、(﹣2,1) C、(﹣2,﹣1) D、(2,1)3. 已知二次函数y=mx2+x+m(m-2)的图像经过原点,则m的值为( )A、0或2 B、0 C、2 D、无法确定4. 函数 的图象经过的象限是( )A、第一、二、三象限 B、第一、二象限 C、第三、四象限 D、第一、二、四象限5. 如图,正方形ABOC的边长为2,反比例函数 的图象过点A,则k的值是( )
 A、2 B、﹣2 C、4 D、﹣46. 如图,正 的顶点A在反比例函数 (x>0)的图象上,则点B的坐标为( )
A、2 B、﹣2 C、4 D、﹣46. 如图,正 的顶点A在反比例函数 (x>0)的图象上,则点B的坐标为( ) A、(2,0) B、( ,0) C、(2 ,0) D、( ,0)7. 如图,抛物线y=ax2+bx+c(a>0)的对称轴是直线x=1,且经过点P(3,0),则a-b+c的值为( )
A、(2,0) B、( ,0) C、(2 ,0) D、( ,0)7. 如图,抛物线y=ax2+bx+c(a>0)的对称轴是直线x=1,且经过点P(3,0),则a-b+c的值为( )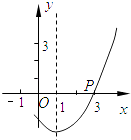 A、0 B、-1 C、1 D、28. 函数y=ax+b和y=ax2+bx+c在同一直角坐标系内的图象大致是( )A、
A、0 B、-1 C、1 D、28. 函数y=ax+b和y=ax2+bx+c在同一直角坐标系内的图象大致是( )A、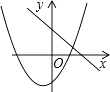 B、
B、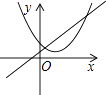 C、
C、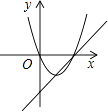 D、
D、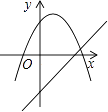 9. 如图△OAP,△ABQ均是等腰直角三角形,点P,Q在函数y= (x>0)的图象上,直角顶点A,B均在x轴上,则点B的坐标为( )
9. 如图△OAP,△ABQ均是等腰直角三角形,点P,Q在函数y= (x>0)的图象上,直角顶点A,B均在x轴上,则点B的坐标为( ) A、( ,0) B、( ,0) C、(3,0) D、( ,0)10. 如图 和 都是边长为2的等边三角形,它们的边 在同一条直线l上,点C,E重合,现将 沿着直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( )
A、( ,0) B、( ,0) C、(3,0) D、( ,0)10. 如图 和 都是边长为2的等边三角形,它们的边 在同一条直线l上,点C,E重合,现将 沿着直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( )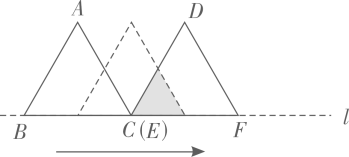 A、
A、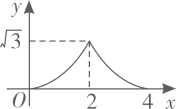 B、
B、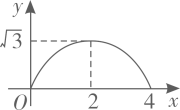 C、
C、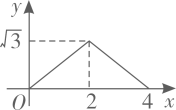 D、
D、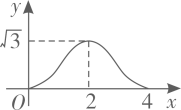
二、填空题
-
11. 抛物线 的顶点在y轴上,则b的值为 .12. 如图,在平面直角坐标系中,点O为坐标原点,平行四边形OABC的顶点A在反比例函数 的图象上,顶点B在反比例函数 的图象上,点C在x轴的正半轴上,则平行四边形OABC的面积是
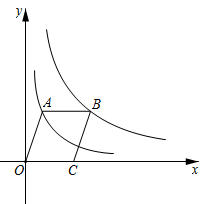 13. 抛物线y=x2+bx+3的对称轴为直线x=1,若关于x的一元二方程x2+bx+3-t=0(t为实数)在-1<x<4的范围内有实数根,则t的取值范围是14. 二次函数y=x2-2x-3,当m-2≤x≤m时函数有最大值5,则m的值可能为
13. 抛物线y=x2+bx+3的对称轴为直线x=1,若关于x的一元二方程x2+bx+3-t=0(t为实数)在-1<x<4的范围内有实数根,则t的取值范围是14. 二次函数y=x2-2x-3,当m-2≤x≤m时函数有最大值5,则m的值可能为三、解答题
-
15. 已知二次函数的顶点坐标为(1,4),且其图象经过点(-2,-5),求此二次函数的解析式。16. 抛物线 .(1)、求顶点坐标,对称轴;(2)、x取何值时,y随x的增大而减小?(3)、x取何值时,y=0;x取何值时,y>0;x取何值时,y<0 .17. 用长为20cm的铁丝,折成一个矩形,设它的一边长为xcm,面积为ycm2 .(1)、求出y与x的函数关系式.(不写自变量的取值范围)(2)、当边长x为多少时,矩形的面积最大,最大面积是多少?18. 已知:已知函数y = y1 +y2 , y1与x成正比例,y2与x成反比例,且当x = 1时,y =-1;当x = 3时,y = 5.求y关于x的函数关系式.19. 关于x的函数y=(m2-1)x2-(2m+2)x+2的图象与x轴只有一个公共点,求m的值.20. 在平面直角坐标系中,二次函数y= x2+bx+c的图象与x轴交于A(-2,0),B(4,0)两点,交y轴于点C,点P是第四象限内抛物线上的一个动点.
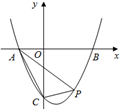 (1)、求二次函数的解析式;(2)、如图,连接AC,PA,PC,若S△PAC= ,求点P的坐标;21. 如图,已知A(-4,n),B(2,-4)是一次函数y1=kx+b的图像和反比例函数 的图像的两个交点
(1)、求二次函数的解析式;(2)、如图,连接AC,PA,PC,若S△PAC= ,求点P的坐标;21. 如图,已知A(-4,n),B(2,-4)是一次函数y1=kx+b的图像和反比例函数 的图像的两个交点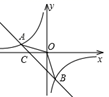 (1)、求反比例函数和一次函数的解析式(2)、求直线与x轴的交点C的坐标及△AOB的面积(3)、当x取何值时,y1=y2;当x取何值时,y1>y222. 如图1,排球场长为18m , 宽为9m , 网高为2.24m . 队员站在底线O点处发球,球从点O的正上方1.9m的C点发出,运动路线是抛物线的一部分,当球运动到最高点A时,高度为2.88m . 即BA=2.88m . 这时水平距离OB=7m , 以直线OB为x轴,直线OC为y轴,建立平面直角坐标系,如图2.
(1)、求反比例函数和一次函数的解析式(2)、求直线与x轴的交点C的坐标及△AOB的面积(3)、当x取何值时,y1=y2;当x取何值时,y1>y222. 如图1,排球场长为18m , 宽为9m , 网高为2.24m . 队员站在底线O点处发球,球从点O的正上方1.9m的C点发出,运动路线是抛物线的一部分,当球运动到最高点A时,高度为2.88m . 即BA=2.88m . 这时水平距离OB=7m , 以直线OB为x轴,直线OC为y轴,建立平面直角坐标系,如图2. (1)、若球向正前方运动(即x轴垂直于底线),求球运动的高度y(m)与水平距离x(m)之间的函数关系式(不必写出x取值范围).并判断这次发球能否过网?是否出界?说明理由;(2)、若球过网后的落点是对方场地①号位内的点P(如图1,点P距底线1m , 边线0.5m),问发球点O在底线上的哪个位置?(参考数据: 取1.4)23. 在平而直角坐标系中,已知点 ,直线 经过点A.抛物线 恰好经过 三点中的两点.(1)、判断点B是否在直线 上.并说明理由;(2)、求 的值;(3)、平移抛物线 ,使其顶点仍在直线 上,求平移后所得抛物线与 轴交点纵坐标的最大值.
(1)、若球向正前方运动(即x轴垂直于底线),求球运动的高度y(m)与水平距离x(m)之间的函数关系式(不必写出x取值范围).并判断这次发球能否过网?是否出界?说明理由;(2)、若球过网后的落点是对方场地①号位内的点P(如图1,点P距底线1m , 边线0.5m),问发球点O在底线上的哪个位置?(参考数据: 取1.4)23. 在平而直角坐标系中,已知点 ,直线 经过点A.抛物线 恰好经过 三点中的两点.(1)、判断点B是否在直线 上.并说明理由;(2)、求 的值;(3)、平移抛物线 ,使其顶点仍在直线 上,求平移后所得抛物线与 轴交点纵坐标的最大值.