高中数学人教新课标A版选修2-2 第一章导数及其计算

试卷更新日期：2020-10-15 类型：单元试卷

进入出卷网下载

一、单选题

1. 函数 $f (x) = x^{4} - 2 x^{3}$ 的图像在点 $(1 ， f (1))$ 处的切线方程为（）

A、 $y = - 2 x - 1$ B、 $y = - 2 x + 1$ C、 $y = 2 x - 3$ D、 $y = 2 x + 1$

查看试题解析
2. 若 $f (x) = x^{4} - \frac{2}{x}$ ，则 $f^{'} (1)$ 等于（）

A、-1 B、2 C、3 D、6

查看试题解析
3. 已知物体位移S（单位：米）和时间t（单位：秒）满足： $S = t^{3} - 2 t + 1$ ，则该物体在 $t = 1$ 时刻的瞬时速度为（）

A、1米/秒 B、2米/秒 C、3米/秒 D、4米/秒

查看试题解析
4. 函数 $y = f (x)$ 的图象如图所示，则阴影部分的面积是（）

A、 $\int_{0}^{1} f (x) d x$ B、 $\int_{0}^{2} f (x) d x$ C、 $\int_{0}^{2} | f (x) | d x$ D、 $\int_{0}^{1} f (x) d x + \int_{1}^{2} f (x) d x$

查看试题解析
5. 已知函数 $f (x) = \ln x$ ，导函数为 $f^{'} (x)$ ，那么 $f^{'} (2)$ 等于（）

A、 $- \frac{1}{4}$ B、 $- \frac{1}{2}$ C、 $\frac{1}{2}$ D、1

查看试题解析
6. 已知函数 $f (x) = \frac{1}{2} x^{2} - \ln x$ ， $f^{'} (x)$ 为 $f (x)$ 的导函数，则 $f^{'} (1)$ 的值为（）

A、-1 B、 $- \frac{1}{2}$ C、0 D、 $\frac{1}{2}$

查看试题解析
7. 函数 $f (x) = (x + 2) e^{x}$ 的单调递增区间是（）

A、 $(- \infty ， 3)$ B、 $(0 ， 3)$ C、 $(- 3 ， 0)$ D、 $(- 3 ， + \infty)$

查看试题解析
8. 已知函数 $f (x)$ 在 $x > 0$ 上可导且满足 $x f^{'} (x) - f (x) > 0$ ，则下列一定成立的为（）

A、 $e f (π) > π f (e)$ B、 $f (π) < f (e)$ C、 $\frac{f (π)}{π} < \frac{f (e)}{e}$ D、 $f (π) > f (e)$

查看试题解析
9. 若点P是曲线 $y = x^{2} - \ln x$ 上任一点，则点P到直线 $x - y - 4 = 0$ 的最小距离是（）

A、 $\sqrt{2}$ B、3 C、 $2 \sqrt{2}$ D、 $2 \sqrt{3}$

查看试题解析
10. 若函数 $f (x) = \frac{1}{2} x^{2} - 9 \ln x$ 在区间 $[a - 1 ， a]$ 上单调递减，则实数a的取值范围是（）

A、 $1 < a \leq 3$ B、 $a \geq 4$ C、 $a \leq 3$ D、 $1 < a \leq 4$

查看试题解析
11. 下列给出四个求导运算：
① $(x - \frac{1}{x})^{'} = \frac{x^{2} - 1}{x^{2}}$ ；② $(x e^{x})^{'} = e^{x} (x + 1)$ ；③ $(\frac{\sin x}{2})^{'} = \frac{\cos x}{4}$ ；④ $(x^{2} - x - l n x)^{'} = \frac{(x - 1) (2 x + 1)}{x}$ .

其中运算结果正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
12. 设 $f (x)$ 是在 $(0 ， + \infty)$ 上的可导函数，且 $f^{'} (x) \geq \frac{2}{x} f (x)$ ， $f (1) = 4$ ， $f (2) = 16$ ，则下列一定不成立的是（）

A、 $f (\frac{3}{2}) = 8$ B、 $f (3) = 40$ C、 $f (4) = 72$ D、 $f (5) = 120$

查看试题解析

二、多选题

13. 已知函数 $y = f (x)$ 的导函数的图象如图所示，下列结论中正确的是（）

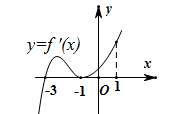A、-1是函数 $f (x)$ 的极小值点 B、-3是函数 $f (x)$ 的极小值点 C、函数 $f (x)$ 在区间 $(- 3 ， 1)$ 上单调递增 D、函数 $f (x)$ 在 $x = 0$ 处切线的斜率小于零

查看试题解析
14. 已知函数 $f (x) = x \ln x$ ，若 $0 < x_{1} < x_{2}$ ，则下列选项正确的是（）

A、 $\frac{f (x_{1}) - f (x_{2})}{x_{1} - x_{2}} < 0$ B、 $x_{1} + f (x_{1}) < x_{2} + f (x_{2})$ C、 $x_{2} f (x_{1}) < x_{1} f (x_{2})$ D、当 $x_{2} > x_{1} > \frac{1}{e}$ 时， $x_{1} f (x_{1}) + x_{2} f (x_{2}) > x_{2} f (x_{1}) + x_{1} f (x_{2})$

查看试题解析
15. 已知 $f (x) = \frac{\ln x}{x}$ ，下列结论正确的是（）

A、 $f (x)$ 在 $(0 ， e)$ 上单调递增 B、 $f (2) > f (3)$ C、 $f (x)$ 的图象在点 $(1 ， 0)$ 处的切线方程为 $y = x$ D、若关于 $x$ 的不等式 ${(\frac{1}{x})}^{\frac{λ}{x}} \leq \frac{1}{27}$ 有正整数解，则 $λ \geq 9$

查看试题解析
16. 已知函数 $f (x) = x \ln x$ ，给出下面四个命题：①函数 $f (x)$ 的最小值为 $- \frac{1}{e}$ ；②函数 $f (x)$ 有两个零点；③若方程 $f (x) = m$ 有一解，则 $m \geq 0$ ；④函数 $f (x)$ 的单调减区间为 $(- \infty ， \frac{1}{e})$ .
则其中错误命题的序号是（）

A、① B、② C、③ D、④

查看试题解析

三、填空题

17. 设函数 $f (x) = \frac{e^{x}}{x + a}$ ．若 $f^{'} (1) = \frac{e}{4}$ ，则a= ．

查看试题解析
18. 曲线 $y = \ln x + x + 1$ 的一条切线的斜率为2，则该切线的方程为.

查看试题解析
19. 已知函数 $f (x) = {\begin{array}{l} e^{2 x} (x > 0) \\ x^{2} + 4 (x \leq 0) \end{array}$ ，若 $\forall x \in R$ ， $f (x) \geq m x$ ，则实数m的取值范围是．

查看试题解析
20. 已知函 $f (x) = a x - \ln x - 1$ ， $g (x) = \frac{x^{3}}{27}$ ，用max{m，n}表示m，n中的最大值，设 $φ (x) = \max {f (x) ， g (x)}$ ．若 $φ (x) \geq \frac{x}{3}$ 在 $(0 ， + \infty)$ 上恒成立，则实数a的取值范围为

查看试题解析

四、解答题

21. 已知函数 $f (x) = (x - k) e^{x}$ ，若 $k = 1$ ，求 $f (x)$ 在 $x = 1$ 处的切线方程.

查看试题解析
22. 已知函数 $f (x) = x^{3} - x^{2} - x + 1$ .

(1)、求 $f (x)$ 在点 $(0 ， f (0))$ 处的切线；

(2)、求 $f (x)$ 在区间 $[0 ， 2]$ 上的最大值和最小值.

查看试题解析
23. 已知函数 $f (x) = 2 x^{3} - 3 a x^{2} - 2$ ，其中 $a \in R$ .

(1)、求 $a = 1$ ，求 $f (x)$ 在 $[0 ， 2]$ 上的最大值和最小值；

(2)、若 $x = 2$ 是函数 $f (x)$ 的一个极值点，求实数 $a$ 的值.

查看试题解析
24. 已知函数 $f (x) = 12 - x^{2}$ ．
（Ⅰ）求曲线 $y = f (x)$ 的斜率等于 $- 2$ 的切线方程；

（Ⅱ）设曲线 $y = f (x)$ 在点 $(t ， f (t))$ 处的切线与坐标轴围成的三角形的面积为 $S (t)$ ，求 $S (t)$ 的最小值．

查看试题解析
25. 已知函数f（x）=2lnx+1．

(1)、若f（x）≤2x+c，求c的取值范围；

(2)、设a>0时，讨论函数g（x）= $\frac{f (x) - f (a)}{x - a}$ 的单调性．

查看试题解析
26. 已知函数 $f (x) = e^{x} + a x^{2} - x$ .

(1)、当a=1时，讨论f（x）的单调性；

(2)、当x≥0时，f（x）≥ $\frac{1}{2}$ x³+1，求a的取值范围.

查看试题解析

高中数学人教新课标A版 选修2-2 第一章 导数及其计算

一、单选题

二、多选题

三、填空题

四、解答题

高中数学人教新课标A版选修2-2 第一章导数及其计算