初中数学苏科版八年级上册3.3勾股定理的简单应用 同步练习
试卷更新日期：2020-10-14 类型：同步测试
一、单选题
-
1. 古代数学的“折竹抵地”问题：“今有竹高九尺，末折抵地，去本三尺，问折者高几何？”意思是：现有竹子高9尺，折后竹尖抵地与竹子底部的距离为3尺，问折处高几尺？即：如图，AB＋AC=9尺，BC=3尺，则AC等于（ ）尺．
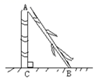A、3.5 B、4 C、4.5 D、52. 如图，有一个水池，其底面是边长为16尺的正方形，一根芦苇AB生长在它的正中央，高出水面部分BC的长为2尺，如果把该芦苇沿与水池边垂直的方向拉向岸边，那么芦苇的顶部B恰好碰到岸边的B′，则这根芦苇AB的长是（ ）
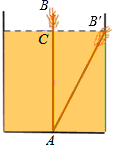A、15尺 B、16尺 C、17尺 D、18尺3. 将一根 24cm 的筷子，置于底面直径为 15cm ， 高 8cm 的装满水的无盖圆柱形水杯中，设筷子浸没在杯子里面的长度为 hcm ， 则 h 的取值范围是（ ）A、h≤15cm B、h≥8cm C、8cm≤h≤17cm D、7cm≤h≤16cm4. 如图，直线l上有三个正方形a，b，c，若a，c的面积分别为5和11，则b的面积为（ ）
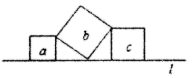A、6 B、8 C、16 D、555. 如图，有两棵树，一棵高12m，另一棵高4m，两树相距15m，一只鸟从一棵树的树梢飞到另一棵树的树梢，至少飞行（ ）
A、8m B、10m C、13m D、17m6. 如图(图在第二页)所示是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3，则最大正方形E的面积是（ ）
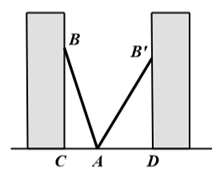
A、13 B、26 C、47 D、947. 如图，小亮将升旗的绳子拉到旗杆底端，绳子末端刚好接触到地面，然后将绳子末端拉到距离旗杆8m处，发现此时绳子末端距离地面2m，则旗杆的高度为（滑轮上方的部分忽略不计）为（ ）
A、12m B、13m C、16m D、17m8. 如图，正 的边长为 ，过点 的直线 ，且 与 关于直线 对称， 为线段 上一动点，则 的最小值是（ ）
A、 B、 C、 D、9. 如图，小明将一张长为20cm，宽为15cm的长方形纸（AE＞DE）剪去了一角，量得AB=3cm，CD=4cm，则剪去的直角三角形的斜边长为（ ）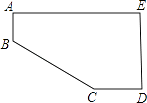
A、5cm B、12cm C、16cm D、20cm10. 如图，长方体的透明玻璃鱼缸，假设其长AD=80cm，高AB=60 cm，水深为AE=40 cm，在水面上紧贴内壁G处有一鱼饵，G在水面线EF上，且EG=60 cm；一小虫想从鱼缸外的A点沿壁爬进鱼缸内G处吃鱼饵，则小动物爬行的最短路线长为（ ）
A、40 cm B、60 cm C、80 cm D、100 cm二、填空题
-
11. 有两根木棒，分别长12cm，5cm，要再在14cm的木棒上取一段，用这三根木棒为边做成直角三角形，这第三根木棒要取的长度是cm.12. 我国古代数学著作《九章算术》有一个问题：一根竹子高1丈，折断后竹子顶端落在离竹子底端3尺处，1丈＝10尺，那么折断处离地面的高度是尺.
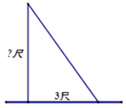13. 如图，在一个高为3米，长为5米的楼梯表面铺地毯，则地毯长度为米.
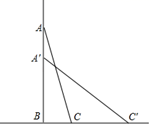
14. 如图，正方形ABCD的边长为4，E是边BC上的一点且BE＝1，P为对角线AC上的一动点，连接PB，PE，当点P在AC上运动时，△PBE周长的最小值是.
15. 如图，一辆小汽车在一条城市街路上直道行驶，某一时刻刚好行驶到路对面车速检测仪A处的正前方30m的C处，过了2s后，测得小汽车与车速检测仪间的距离为50m，则这辆小汽车的速度是m/s.
16. 如图，圆柱形容器高为18cm，底面周长为24cm，在杯内壁离杯底4cm的点B处有乙滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿2cm与蜂蜜相对的点A处，则蚂蚁从外币A处到达内壁B处的最短距离为.
三、解答题
-
17. 如图，小巷左右两侧是竖直的墙，一架梯子 斜靠在左墙时，梯子底端到左墙角的距离 为0.7米，顶端到地面距离 为2.4米，如果保持梯子底端位置不动，将梯子斜靠在右墙时，顶端到地面距离 为2米，求小巷的宽度 .
