初中数学苏科版八年级上册3.2勾股定理逆定理同步练习

试卷更新日期：2020-10-13 类型：同步测试

进入出卷网下载

一、单选题

1. 下列各线段的长，能构成直角三角形的是 $($ $)$

A、2，3，4 B、5，12，13 C、4，6，9 D、5，11，13

查看试题解析
2. 在△ABC中，∠A、∠B、∠C的对边分别为a、b、c，下列条件中不能说明△ABC是直角三角形的是（）

A、a＝3² ， b＝4² ， c＝5² B、a＝9，b＝12，c＝15 C、∠A：∠B：∠C＝5：2：3 D、∠C﹣∠B＝∠A

查看试题解析
3. 已知△ABC的三边分别是6，8，10，则△ABC斜边上的高是（）

A、2 B、2.4 C、4 D、4.8

查看试题解析
4. $△ A B C$ 的三边 $B C = a, A C = b, A B = c$ ，且 $(a + c) (a - c) - b^{2} = 0$ ，下列结论正确的是（）

A、 $△ A B C$ 是等腰直角三角形且 $∠ C = 90 °$ B、 $△ A B C$ 是直角三角形或等腰三角形 C、 $△ A B C$ 是直角三角形，且 $∠ C = 90 °$ D、 $△ A B C$ 是直角三角形，且 $∠ A = 90 °$

查看试题解析
5. 如图，已知 $△ A B C$ 中， $A B = 10 ， A C = 8 ， B C = 6 ， A B$ 的垂直平分线分别交 $A C ， A B$ 于 $D ， E ，$ 连接 $B D$ ，则 $C D$ 的长为（）

A、 $1$ B、 $\frac{5}{4}$ C、 $\frac{7}{4}$ D、 $\frac{25}{4}$

查看试题解析
6. 有下面的判断：
①若△ABC中，a²＋b²≠c² ，则△ABC不是直角三角形；②△ABC是直角三角形，∠C=90°，则a²＋b²=c²；③若△ABC中，a²－b²=c² ，则△ABC是直角三角形；④若△ABC是直角三角形，则(a＋b)(a－b)=c².其中判断正确的有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
7. 如下图五根小木棒，其长度分别为7，15，20，24，25，现将他们摆成两个直角三角形，其中正确的是（）

A、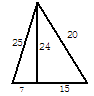 B、 C、 D、

查看试题解析
8. 三角形的三边a，b，c满足(a＋b)²－c²＝2ab，则此三角形是（）．

A、锐角三角形 B、直角三角形 C、钝角三角形 D、等边三角形

查看试题解析
9. 在⊿ $A B C$ 中，若 $a = n^{2} - 1, b = 2 n, c = n^{2} + 1$ ，则⊿ $A B C$ 是（）

A、锐角三角形 B、钝角三角形 C、等腰三角形 D、直角三角形

查看试题解析
10. 已知 $a$ ， $b$ ， $c$ 是 $△ A B C$ 的三边，如果满足 $a^{2} c^{2} - b^{2} c^{2} = a^{4} - b^{4}$ ，则三角形的形状是 $($ $)$

A、等腰三角形 B、直角三角形 C、等腰三角形或直角三角形 D、等腰直角三角形

查看试题解析

二、填空题

11. 一个三角形的三边的比为5∶12∶13，它的周长为60cm，则它的面积是．

查看试题解析
12. 已知△ABC的三边长为a、b、c，满足a+b=10，ab=18，c=8，则此三角形为三角形．

查看试题解析
13. 如果△ABC的三边长a、b、c满足关系式（a+2b﹣60）²+|b﹣18|+|c﹣30|=0，则△ABC的形状是．

查看试题解析
14. 在△ABC 中，若 $a^{2} + b^{2} = 25 ， a^{2} - b^{2} = 7 ， c = 5$ ，则最长边上的高为．

查看试题解析
15. 已知a，b，c为三角形的三边，且满足a²c²-b²c²=a⁴-b⁴ ，那么它的形状是．

查看试题解析
16. 已知：如图，四边形ABDC，AB＝4，AC＝3，CD＝12，BD＝13，∠BAC＝90°．则四边形ABDC的面积是．

查看试题解析
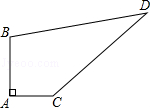17. 如图，已知CD=6m，AD=8m，∠ADC=90°，BC=24m，AB=26m．图中阴影部分的面积=m² ．

查看试题解析
18. 如图，△ABC是边长3cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB、BC方向匀速移动，点P的速度都是1cm/s，点Q的速度都是2cm/s当点P到达点B时，P、Q两点停止．当t=时，△PBQ是直角三角形．

查看试题解析

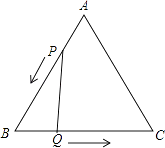
三、解答题

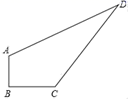
19. 若△ABC三边长为a，b，c满足a²+b²+c²+200=12a+16b+20c，试判断△ABC的形状．

查看试题解析
20. 已知：如图，四边形ABCD中，∠B=90°，AB＝3，BC＝4，CD＝12，AD＝13，求四边形ABCD的面积?

查看试题解析
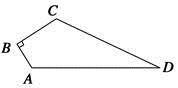21. 如图，四边形ABCD中， $A B = 4 c m$ ， $B C = 3 c m$ ， $C D = 12 c m$ ， $D A = 13 c m$ ， $∠ A B C = 90^{\circ}$ ，求四边形ABCD的面积.

查看试题解析
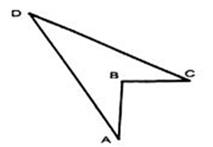22. 如图，四边形ABCD中，∠B＝90°，AB＝2，BC＝1，CD＝2，AD＝3，连接AC ．

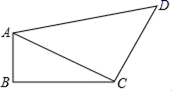(1)、求AC的长；

(2)、判断三角形ACD的形状，并求出四边形ABCD的面积．

查看试题解析
23. 如图，某住宅小区在施工过程中留下了一块空地（图中的四边形ABCD），经测量，在四边形ABCD中，AB＝3m，BC＝4m，CD＝12m，DA＝13m，∠B＝90°．

(1)、△ACD是直角三角形吗？为什么？

(2)、小区为美化环境，欲在空地上铺草坪，已知草坪每平方米80元，试问铺满这块空地共需花费多少元？

查看试题解析
24. 已知在 $Δ A B C$ 中，D是 $B C$ 的中点， $D E ⊥ B C$ ，垂足为D，交 $A B$ 于点E，且 $B E^{2} - A E^{2} = A C^{2}$ .

(1)、求 $∠ A$ 的度数；

(2)、若 $D E = 3$ ， $B D = 4$ ，求 $A E$ 的长.

查看试题解析

初中数学苏科版八年级上册3.2勾股定理逆定理 同步练习

一、单选题

二、填空题

三、解答题

初中数学苏科版八年级上册3.2勾股定理逆定理同步练习