海南省省直辖县级行政单位乐东黎族自治县2020届九年级上学期数学期中考试试卷

试卷更新日期：2020-10-13 类型：期中考试

进入出卷网下载

一、选择题

1. 下面的图形中，既是轴对称图形又是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 下列方程是一元二次方程的是（）

A、 $x^{2} + 2 y - 3 = 0$ B、 $x^{2} - 3 = 0$ C、 ${(x^{2} + 3)}^{2} = 9$ D、 $x^{2} + \frac{1}{x^{2}} = 4$

查看试题解析
3. 平面直角坐标系中，与点（2，﹣3）关于原点中心对称的点是（）

A、（﹣3，2） B、（3，﹣2） C、（﹣2，3） D、（2，3）

查看试题解析
4. 关于x的一元二次方程x²+bx+c＝0的两个实数根分别为2和﹣3，则（）

A、b＝1，c＝﹣6 B、b＝﹣1，c＝﹣6 C、b＝5，c＝﹣6 D、b＝﹣1，c＝6

查看试题解析
5. 抛物线y＝x²向左平移3个单位，再向下平移2个单位后，所得的抛物线表达式是（　　）

A、y＝（x﹣3）²﹣2 B、y＝（x﹣3）²+2 C、y＝（x+3）²﹣2 D、y＝（x+3）²+2

查看试题解析
6. 用配方法解方程x²+6x+11=0，下面配方正确的是（）

A、（x+3）²=2 B、（x+3）²=﹣2 C、（x﹣3）²=2 D、（x﹣3）²=﹣2

查看试题解析
7. 对于二次函数y＝（x﹣1）²+2的图象，下列说法正确的是（　　）

A、开口向下 B、顶点坐标是（1，2） C、对称轴是x＝﹣1 D、与x轴有两个交点

查看试题解析
8. 从5点15分到5点20分，分针旋转的度数为（）

A、20° B、26° C、30° D、36°

查看试题解析
9. 关于x的一元二次方程2x²+3x﹣1=0的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定

查看试题解析
10. 已知二次函数 $y = (k - 3) x^{2} + 2 x + 1$ 的图象与 $x$ 轴有两个交点，则 $k$ 的取值范围是（）.

A、 $k < 4$ 且k≠3 B、 $k \leq 4$ C、 $k > 4$ D、 $k \geq 4$

查看试题解析
11. 如图，平行四边形ABCD可以看作是由下列哪个三角形旋转得到的（　　）

A、△AOB B、△DOC C、△COB D、△BCD

查看试题解析
12. 如图，二次函数y＝ax²+bx+c（a≠0）图象的一部分，对称轴为直线x＝ $\frac{1}{2}$ ，且经过点（2，0），下列说法：
①abc＜0；

②a+b＝0；

③4a+2b+c＜0；

④若（﹣2，y₁），（﹣3，y₂）是抛物线上的两点，则y₁＜y₂ ，

其中说法正确的是（　　）

A、①②④ B、③④ C、①③④ D、①②

查看试题解析

二、填空题

13. 把方程3x²＝5x+2化为一元二次方程的一般形式是.

查看试题解析
14. 抛物线y=﹣x²﹣2x+1，其图象的开口，当x=时，y有最值是．

查看试题解析
15. 如图，△ABC≌△ADE，∠C与∠AED都是直角，点E在AB上，∠D=30°，那么△ABC绕着点逆时针方向旋转度能与△ADE重合．

查看试题解析
16. 关于x的一元二次方程2x²-4x+m-1=0有两个相等的实数根，则m的值为。

查看试题解析

三、解答题

17. 用适当的方法解下列方程　

(1)、 $x^{2} - 6 x - 16 = 0$

(2)、3（x﹣2）²＝2（2﹣x）.

查看试题解析
18. 已知：关于x的方程 $x^{2} - (k + 2) x + 2 k = 0$ ，

(1)、求证：无论k取任何实数值，方程总有实数根；

(2)、若等腰三角形ABC的一边长a=1，两个边长b，c恰好是这个方程的两个根，求△ABC的周长．

查看试题解析
19.
如图，在宽为20米、长为30米的矩形地面上修建两条同样宽的道路，余下部分作为耕地．若耕地面积需要551米² ，则修建的路宽应为多少米？

查看试题解析
20. 如图，在正方形网格中，△ABC各顶点都在格点上，点A，C的坐标分别为（﹣5，1）、（﹣1，4），结合所给的平面直角坐标系解答下列问题：

（ 1 ）画出△ABC关于y轴对称的△A₁B₁C₁；

（ 2 ）画出△ABC关于原点O对称的△A₂B₂C₂；

（ 3 ）点C₁的坐标是 ▲ ；点C₂的坐标是 ▲ ；

（ 4 ）试判断：与是否关于x轴对称?（只需写出判断结果）.

查看试题解析
21. 某大学毕业生响应国家自主创业的号召，投资开办了一个装饰品商店，某种商品每件的进价为20元，现在售价为每件40元，每周可卖出150件，市场调查发现：如果每件的售价每降价1元(售价不低于20元)，那么每周多卖出25件，设每件商品降价x元，每周的利润为y元.

(1)、请写出利润y与售价x之间的函数关系式.

(2)、当售价为多少元时，利润可达4000元？

(3)、应如何定价才能使利润最大？

查看试题解析
22.
已知：如图，二次函数y=ax²+bx+c的图象与x轴交于A，B两点，其中A点坐标为（﹣1，0），点C（0，5），另抛物线经过点（1，8），M为它的顶点．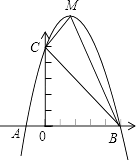

(1)、求抛物线的解析式；

(2)、求△MCB的面积S_△_MCB ．

(3)、在坐标轴上，是否存在点N，满足△BCN为直角三角形？如存在，请直接写出所有满足条件的点N．

查看试题解析