海南省琼中黎族苗族自治县2020届九年级上学期数学期中考试试卷
试卷更新日期:2020-10-13 类型:期中考试
一、选择题
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是A、
 B、
B、 C、
C、 D、
D、 2. 二次函数 的最小值是 ( )A、 2 B、2 C、 1 D、13. 在平面直角坐标系中,将△AOB绕原点O顺时针旋转180°后得到△A1OB1 , 若点B的坐标为(2,1),则点B的对应点B1的坐标为( )A、(1,2) B、(2,-1) C、(-2,1) D、(-2,-1)4. 方程x2 = 2x的解是( )A、x=2 B、x1=
2. 二次函数 的最小值是 ( )A、 2 B、2 C、 1 D、13. 在平面直角坐标系中,将△AOB绕原点O顺时针旋转180°后得到△A1OB1 , 若点B的坐标为(2,1),则点B的对应点B1的坐标为( )A、(1,2) B、(2,-1) C、(-2,1) D、(-2,-1)4. 方程x2 = 2x的解是( )A、x=2 B、x1= ,x2= 0
C、x1=2,x2=0
D、x = 0
5. 用配方法解方程 ,变形后的结果正确的是( )A、 B、 C、 D、6. 一元二次方程 的根的情况是A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定7. 如图, 绕点O逆时针旋转 到 的位置,已知 ,则 等于( )
,x2= 0
C、x1=2,x2=0
D、x = 0
5. 用配方法解方程 ,变形后的结果正确的是( )A、 B、 C、 D、6. 一元二次方程 的根的情况是A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定7. 如图, 绕点O逆时针旋转 到 的位置,已知 ,则 等于( )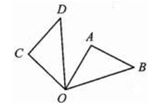 A、 B、 C、 D、8. 把抛物线y=3 向左平移2个单位,再向上平移1个单位,所得的抛物线的解析式是( )A、y=3 +1 B、y=3 ﹣1 C、y=3 +1 D、y=3 ﹣19. 如图,将 绕点A按顺时针旋转一定角度得到 ,点B的对应点D恰好落在BC边上 若 , ,则CD的长为
A、 B、 C、 D、8. 把抛物线y=3 向左平移2个单位,再向上平移1个单位,所得的抛物线的解析式是( )A、y=3 +1 B、y=3 ﹣1 C、y=3 +1 D、y=3 ﹣19. 如图,将 绕点A按顺时针旋转一定角度得到 ,点B的对应点D恰好落在BC边上 若 , ,则CD的长为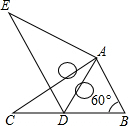 A、 B、 C、 D、110. 已知一元二次方程x2-8x+15=0的两个解恰好分别是等腰△ABC的底边长和腰长,则△ABC的周长为( )
A、 B、 C、 D、110. 已知一元二次方程x2-8x+15=0的两个解恰好分别是等腰△ABC的底边长和腰长,则△ABC的周长为( )
A、13 B、11或13 C、11 D、1211. 对于抛物线 ,下列判断正确的是( )A、抛物线的开口向上 B、抛物线的顶点坐标是 C、对称轴为直线 D、当 时,y随x的增大而增大12. 当a>0,b<0,c>0时,下列图象有可能是抛物线y=ax2+bx+c的是( )A、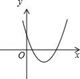 B、
B、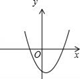 C、
C、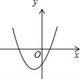 D、
D、
二、填空题
-
13. 当x=时,分式 的值为0.14. 如图,可以看作是由其中一个菱形至少经过次旋转得到的,旋转角的度数是.
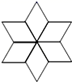 15. y=﹣2x2的图象上有三个点(﹣1,y1),(2,y2),(3,y3),则y1 , y2 , y3的大小关系为.16. 如图,含有30°的直角三角板△ABC,∠BAC=90°,∠C=30°,将△ABC绕着点A逆时针旋转,得到△AMN,使得点B落在BC边上的点M处,过点N的直线l∥BC,则∠1=.
15. y=﹣2x2的图象上有三个点(﹣1,y1),(2,y2),(3,y3),则y1 , y2 , y3的大小关系为.16. 如图,含有30°的直角三角板△ABC,∠BAC=90°,∠C=30°,将△ABC绕着点A逆时针旋转,得到△AMN,使得点B落在BC边上的点M处,过点N的直线l∥BC,则∠1=.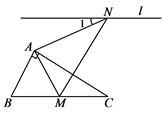
三、解答题
-
17.(1)、解方程:3x(x﹣2)﹣2(x﹣2)=0(2)、解方程:2x2﹣3x﹣5=018. 某电脑销售商试销某一品牌电脑1月份的月销售额为400000,现为了扩大销售,销售商决定降价销售,在原来1月份平均销售量的基础上,经2月份的市场调查,3月份调整价格后,月销售额达到576000元.求1月份到3月份销售额的月平均增长率.19. 已知二次函数的图象经过(﹣1,0),(3,0),(1,﹣5)三点.(1)、求该二次函数的解析式;(2)、求该图象的顶点坐标.20. 在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣4,5),C(﹣5,2).
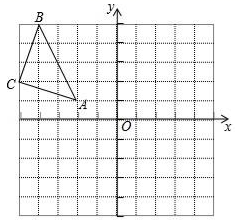 (1)、画出△ABC关于原点O成中心对称的△A1B1C1;(2)、写出△A1B1C1的顶点坐标;(3)、求出△A1B1C1的面积.21. 如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上点(点D与A,B不重合),连结CD,将线段CD绕点C按逆时针方向旋转90°得到线段CE,连结DE交BC于点F,连接BE.
(1)、画出△ABC关于原点O成中心对称的△A1B1C1;(2)、写出△A1B1C1的顶点坐标;(3)、求出△A1B1C1的面积.21. 如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上点(点D与A,B不重合),连结CD,将线段CD绕点C按逆时针方向旋转90°得到线段CE,连结DE交BC于点F,连接BE.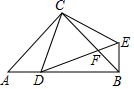 (1)、求证:△ACD≌△BCE;(2)、当AD=BF时,求∠BEF的度数;(3)、若AB=4,AD=1,求CD的长.22. 如图,抛物线y=ax2+2x+c经过点A(0,3),B(﹣1,0),请解答下列问题:
(1)、求证:△ACD≌△BCE;(2)、当AD=BF时,求∠BEF的度数;(3)、若AB=4,AD=1,求CD的长.22. 如图,抛物线y=ax2+2x+c经过点A(0,3),B(﹣1,0),请解答下列问题: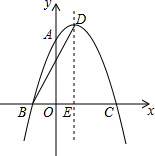 (1)、求抛物线的解析式;(2)、抛物线的顶点为点D,对称轴与x轴交于点E,连接BD,求BD的长;(3)、点F在抛物线上运动,是否存在点F,使△BFC的面积为6,如果存在,求出点F的坐标;如果不存在,请说明理由.
(1)、求抛物线的解析式;(2)、抛物线的顶点为点D,对称轴与x轴交于点E,连接BD,求BD的长;(3)、点F在抛物线上运动,是否存在点F,使△BFC的面积为6,如果存在,求出点F的坐标;如果不存在,请说明理由.