湖北武汉硚口区2021届九年级上学期数学9月月考试卷
试卷更新日期:2020-10-13 类型:月考试卷
一、选择题
-
1. 方程x2-3x=4的二次项系数、一次项系数、常数项分别为( )A、1、-3、4 B、1、-3、-4 C、-3、1、4 D、-3、1、-42. 已知x=-2是关于x的方程2x2-4a=0的一个解,则a的值是( )A、-1 B、1 C、-2 D、23. 将一元二次方程 化成 (a,b为常数)的形式,则a,b的值分别是( )A、 ,21 B、 ,11 C、4,21 D、 ,694. 上海世博会的某纪念品原价168元,连续两次降价a%后售价为128元,下面所列方程中正确的是( )A、168(1+a%)2=128 B、168(1-a%)2=128 C、168(1-2a%)=128 D、168(1-a2%)=1285. 将抛物线 向上平移3个单位长度,再向右平移5个单位长度,所得的抛物线为( )A、 B、 C、 D、6. 如图,把一块长为40cm,宽为30cm的矩形硬纸板的四角剪去四个相同小正方形,然后把纸板的四边沿虚线折起,并用胶带粘好,即可做成一个无盖纸盒.若该无盖纸盒的底面积为600cm2 , 设剪去小正方形的边长为xcm,则可列方程为( )
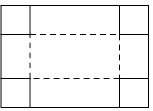 A、(30﹣2x)(40﹣x)=600 B、(30﹣x)(40﹣x)=600 C、(30﹣x)(40﹣2x)=600 D、(30﹣2x)(40﹣2x)=6007. 如图,正方形三个顶点的坐标依次为(3,1)、(1,1)、(1,3).若抛物线y=ax2的图象与正方形的边有公共点,则实数a的取值范围是( )
A、(30﹣2x)(40﹣x)=600 B、(30﹣x)(40﹣x)=600 C、(30﹣x)(40﹣2x)=600 D、(30﹣2x)(40﹣2x)=6007. 如图,正方形三个顶点的坐标依次为(3,1)、(1,1)、(1,3).若抛物线y=ax2的图象与正方形的边有公共点,则实数a的取值范围是( )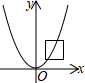 A、 ≤a≤3 B、 ≤a≤1 C、 ≤a≤3 D、 ≤a≤18. 关于x的方程 ( 为常数)根的情况下,下列结论中正确的是( )A、两个正根 B、两个负根 C、一个正根,一个负根 D、无实数根9. 抛物线y=ax2+bx+c(a、b、c为常数,a<0)经过A(2,0)、B(-4,0)两点,若点P(-5,y1)、Q(π,y2)、R(5,y3)该抛物线上,则( )A、y1<y2<y3 B、y1=y3<y2 C、y1<y3<y2 D、y3<y2<y110. 如图 和 都是边长为2的等边三角形,它们的边 在同一条直线l上,点C,E重合,现将 沿着直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( )
A、 ≤a≤3 B、 ≤a≤1 C、 ≤a≤3 D、 ≤a≤18. 关于x的方程 ( 为常数)根的情况下,下列结论中正确的是( )A、两个正根 B、两个负根 C、一个正根,一个负根 D、无实数根9. 抛物线y=ax2+bx+c(a、b、c为常数,a<0)经过A(2,0)、B(-4,0)两点,若点P(-5,y1)、Q(π,y2)、R(5,y3)该抛物线上,则( )A、y1<y2<y3 B、y1=y3<y2 C、y1<y3<y2 D、y3<y2<y110. 如图 和 都是边长为2的等边三角形,它们的边 在同一条直线l上,点C,E重合,现将 沿着直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( ) A、
A、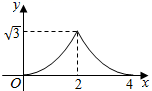 B、
B、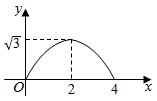 C、
C、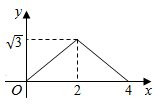 D、
D、
二、填空题
-
11. 方程x2﹣4=0的解是 ,
化简:(1﹣a)2+2a= .
12. 某种植物的主干长出若干相同数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是73,求每个支干又长出多少小分支?如果设每个支干又长出 个小分支,那么依题意可得方程为.13. 抛物线y=x2+2x+5的顶点坐标是14. 直线y=x+a不经过第二象限,则关于x的方程ax2+2x+1=0实数解的个数是15. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=-1,下列结论:① b2>4ac;② abc>0;③ a-c<0;④ am2+bm≥a-b(m为任意实数),其中正确的结论是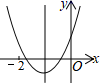 16. 如图,在矩形纸片ABCD中,AB=5,E为边CD上一点,DE=2.将△BCE沿BE折叠,点C落在F处,BF交AD于点M.若∠MEB=45°,则BC=
16. 如图,在矩形纸片ABCD中,AB=5,E为边CD上一点,DE=2.将△BCE沿BE折叠,点C落在F处,BF交AD于点M.若∠MEB=45°,则BC=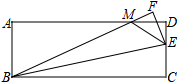
三、解答题
-
17. 解方程:(1)、(2)、x2+4x-3=018. 参加一次商品交易会的两家公司之间都签订了一份合同,所有公司共签订了45份合同,共有多少家公司参加商品交易会?19. 去年某商店“十一黄金周”进行促销活动期间,前六天的总营业额为450万元,第七天的营业额是前六天总营业额的12%.(1)、求该商店去年“十一黄金周”这七天的总营业额;(2)、去年,该商店7月份的营业额为350万元,8、9月份营业额的月增长率相同,“十一黄金周”这七天的总营业额与9月份的营业额相等.求该商店去年8、9月份营业额的月增长率.20. 若x1、x2是一元二次方程x2-2x+k+2=0的两个实数根,满足 ,求k的值.21.(1)、抛物线y=ax2+c经过点A (2,3),点B (-1,-3)两点,求该抛物线的解析式.(2)、如图,要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3 m,水柱落地处离池中心3 m,水管应多长?
 22. 某单位不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边靠墙,可利用的墙长不超过18 m,另外三边由36 m长的栅栏围成.设矩形ABCD空地中,垂直于墙的边AB=x m,面积为y m2(如图).
22. 某单位不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边靠墙,可利用的墙长不超过18 m,另外三边由36 m长的栅栏围成.设矩形ABCD空地中,垂直于墙的边AB=x m,面积为y m2(如图). (1)、求y与x之间的函数关系式,并写出自变量x的取值范围.(2)、若矩形空地的面积为160 m2 , 求x的值.(3)、矩形空地的面积能否为164 m2 , 若能,求x的值;不能,请说明理由.23. 已知正方形ABCD和等腰Rt△CEF,∠CEF=90°,CE=EF,连接AF.(1)、如图,点E在CD边上.若EF=2,AD=6,求AF的长.
(1)、求y与x之间的函数关系式,并写出自变量x的取值范围.(2)、若矩形空地的面积为160 m2 , 求x的值.(3)、矩形空地的面积能否为164 m2 , 若能,求x的值;不能,请说明理由.23. 已知正方形ABCD和等腰Rt△CEF,∠CEF=90°,CE=EF,连接AF.(1)、如图,点E在CD边上.若EF=2,AD=6,求AF的长. (2)、如图,点E在CD边上,点G为AF的中点,求证:AD+EF= BG.
(2)、如图,点E在CD边上,点G为AF的中点,求证:AD+EF= BG. (3)、如图,点E在BC边上,点G为AF的中点.若BE=4,CE=2,则BG=
(3)、如图,点E在BC边上,点G为AF的中点.若BE=4,CE=2,则BG= 24. 抛物线y=ax2-2ax-3a(a<0)交x轴于点A、B,交y轴于点C,它的对称轴交x轴于点E.(1)、直接写出点E的坐标为(2)、如图,直线y=x与抛物线交于点M、N,求OM·ON的值.
24. 抛物线y=ax2-2ax-3a(a<0)交x轴于点A、B,交y轴于点C,它的对称轴交x轴于点E.(1)、直接写出点E的坐标为(2)、如图,直线y=x与抛物线交于点M、N,求OM·ON的值. (3)、如图2,过点C作CD∥x轴交抛物线于点D,连接DE并延长交y轴于点F,交抛物线于点G.直线AF交CD于点H,交抛物线于点K,连接HE、GK,求证:HE∥GK.
(3)、如图2,过点C作CD∥x轴交抛物线于点D,连接DE并延长交y轴于点F,交抛物线于点G.直线AF交CD于点H,交抛物线于点K,连接HE、GK,求证:HE∥GK.