湖北省孝感市三校2021届九年级上学期数学第一次月考试卷
试卷更新日期:2020-10-13 类型:月考试卷
一、选择题
-
1. 将一元二次方程 化成 (a,b为常数)的形式,则a,b的值分别是( )A、 ,21 B、 ,11 C、4,21 D、 ,692. 定义运算: .例如 .则方程 的根的情况为( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、只有一个实数根3. 已知m、n、4分别是等腰三角形(非等边三角形)三边的长,且m、n是关于x的一元二次方程 ﹣6x+k+2=0的两个根,则k的值等于( )A、7 B、7或6 C、6或﹣7 D、64. 将抛物线 向左平移3个单位长度,再向下平移2个单位长度,得到抛物线的解析式是( )A、 B、 C、 D、5. 已知(-3,y1),(-2,y2),(1,y3)是抛物线y=-3x2-12x+m上的点,则( )A、y3<y2<y1 B、y3<y1<y2 C、y2<y3<y1 D、y1<y3<y26. 已知函数 和 (a是常数,且a≠0),函数y1和y2的图象可能是( )A、
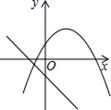 B、
B、 C、
C、 D、
D、 7. 某医院内科病房有护士x人,每2人一班,轮流值班,每8小时换班一次,某两人同值一班后,到下次两人再同班,最长需要的天数是70天,则 ( )A、 B、 C、 D、8. 某市从2017年开始大力发展“竹文化”旅游产业.据统计,该市2017年“竹文化”旅游收入约为2亿元.预计2019“竹文化”旅游收入达到2.88亿元,据此估计该市2018年、2019年“竹文化”旅游收入的年平均增长率约为( )
7. 某医院内科病房有护士x人,每2人一班,轮流值班,每8小时换班一次,某两人同值一班后,到下次两人再同班,最长需要的天数是70天,则 ( )A、 B、 C、 D、8. 某市从2017年开始大力发展“竹文化”旅游产业.据统计,该市2017年“竹文化”旅游收入约为2亿元.预计2019“竹文化”旅游收入达到2.88亿元,据此估计该市2018年、2019年“竹文化”旅游收入的年平均增长率约为( )
A、2% B、4.4% C、20% D、44%9. 点P(m,n)在以y轴为对称轴的二次函数y=x2+ax+4的图象上.则m﹣n的最大值等于( )A、 B、4 C、﹣ D、﹣10. 如图,已知抛物线 的对称轴为直线 .给出下列结论: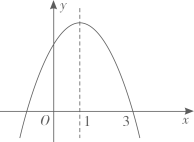
① ; ② ; ③ ; ④ .
其中,正确的结论有( )
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 抛物线 的顶点坐标为 .12. 若 ,则 .13. 若x1 , x2是方程x2﹣4x﹣2020=0的两个实数根,则代数式x12﹣2x1+2x2的值等于.14. 下表中 与 的数据满足我们初中学过的某种函数关系,其函数表达式为.
……
……
……
……
15. 若x=4是二次方程x2+ax﹣4b=0的解,则代数式a﹣b的值为.16. 如图,在平面直角坐标系中,点A是抛物线 与y轴的交点,点B是这条抛物线上的另一点,且AB∥x轴,则以AB为边的等边三角形ABC的周长为.
三、解答题
-
17. 解方程(1)、x2-5x=0(2)、(x-3)(x+3)=2x18. 已知二次函数的图象过点(0,3),顶点坐标为(﹣4,11).(1)、求这个二次函数的表达式;(2)、求这个二次函数图象与x轴交点坐标.19. 在平面直角坐标系xOy中,抛物线y=x2-2mx+m2-m+2的顶点为D.线段AB的两个端点分别为A(-3,m),B(1,m).(1)、求点D的坐标(用含m的代数式表示);(2)、若该抛物线经过点B(1,m),求m的值;(3)、若线段AB与该抛物线只有一个公共点,结合函数的图象,求m的取值范围.20. 已知关于x的一元二次方程 有两个不相等的实数根.(1)、求k的取值范围;(2)、若方程的两个不相等实数根是a,b,求 的值.21. 已知关于 的一元二次方程 ,其中 、 、 分别为 三边的长.(1)、如果 是方程的根,试判断 的形状,并说明理由;(2)、如果 是等边三角形,试求这个一元二次方程的根.22. 某公司展销如图所示的长方形工艺品,该工艺品长60cm宽40cm,中间镶有宽度相同的三条丝绸花边.
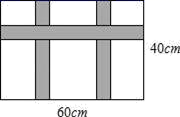 (1)、若丝绸花边的面积(阴影面积)为650cm2 , 求丝绸花边的宽度;(2)、已知该工艺品的成本是40元/件,如果以单价100元/件销售,那么每天可售出200件,另每天还需支付各种费用2000元,根据销售经验,如果将销售单价降低1元,每天可多售出20件,同时,为了完成销售任务,该公司每天至少要销售800件.
(1)、若丝绸花边的面积(阴影面积)为650cm2 , 求丝绸花边的宽度;(2)、已知该工艺品的成本是40元/件,如果以单价100元/件销售,那么每天可售出200件,另每天还需支付各种费用2000元,根据销售经验,如果将销售单价降低1元,每天可多售出20件,同时,为了完成销售任务,该公司每天至少要销售800件.(ⅰ)若想每天获利18000元,该公司应该把销售单价定为多少元?
(ⅱ)该公司应该把销售单价定为多少元,才能使每天所获销售利润最大?最大利润是多少?
23. 定义:若关于x的一元二次方程ax2+bx+c=0(a≠0)的两个实数根为x1 , x2(x1<x2),分别以x1 , x2为横坐标和纵坐标得到点M(x1 , x2),则称点M为该一元二次方程的衍生点.(1)、若关于x的一元二次方程为x2-2(m-1)x+m2-2m=0.①求证:不论m为何值,该方程总有两个不相等的实数根,并求出该方程的衍生点M的坐标;
②直线l1:y=x+5与x轴交于点A,直线l2过点B(1,0),且l1与l2相交于点C(-1,4),若由①得到的点M在△ABC的内部,求m的取值范围.
(2)、是否存在b,c,使得不论k(k≠0)为何值,关于x的方程x2+bx+c=0的衍生点M始终在直线y=kx+3(2-k)的图象?若有,求出b+c的值;若没有,说明理由.24. 如图,抛物线过点A(0,1)和C,顶点为D,直线AC与抛物线的对称轴BD的交点为B( ,0),平行于y轴的直线EF与抛物线交于点E,与直线AC交于点F,点F的横坐标为 ,四边形BDEF为平行四边形.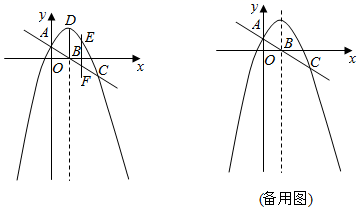 (1)、求点F的坐标及抛物线的解析式;(2)、若点P为抛物线上的动点,且在直线AC上方,当△PAB面积最大时,求点P的坐标及△PAB面积的最大值;(3)、在抛物线的对称轴上取一点Q,同时在抛物线上取一点R,使以AC为一边且以A,C,Q,R为顶点的四边形为平行四边形,求点Q和点R的坐标.
(1)、求点F的坐标及抛物线的解析式;(2)、若点P为抛物线上的动点,且在直线AC上方,当△PAB面积最大时,求点P的坐标及△PAB面积的最大值;(3)、在抛物线的对称轴上取一点Q,同时在抛物线上取一点R,使以AC为一边且以A,C,Q,R为顶点的四边形为平行四边形,求点Q和点R的坐标.