江苏省兴化市四校2020-2021学年八年级上学期数学第一次月考联考试卷
试卷更新日期：2020-10-13 类型：月考试卷
一、选择题
-
1. 低碳环保理念深入人心，共享单车已成为出行新方式．下列共享单车图标，是轴对称图形的是（ ）A、
B、
C、
D、
2.如图，某同学把一块三角形的玻璃打破成了三块，现要到玻璃店去配一块大小、形状完全相同的玻璃，那么他可以（ ）
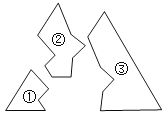A、带①去 B、带②去 C、带③去 D、带①和②去3. 小天从镜子里看到镜子对面的电子钟如下图所示，则此时的实际时间是 （ ）
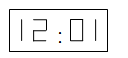A、21：10 B、10：21 C、10：51 D、12：014. 如图，工人师傅砌门时，常用木条EF固定矩形门框ABCD，使其不变形，这种做法的根据是（ ）
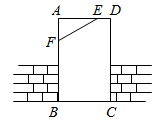A、两点之间线段最短 B、矩形的对称性 C、矩形的四个角都是直角 D、三角形的稳定性5. 如图，OP平分∠MON，PA⊥ON于点A，点Q是射线OM上的一个动点，若PA=2，则PQ的最小值为（ ）
A、1 B、2 C、3 D、46. 已知△ABC≌△A'B'C，∠A＝40°，∠CBA＝60°，A'C交边AB于P（点P不与A、B重合）.BO、CO分别平分∠CBA，∠BCP，若m°＜∠BOC＜n°，则n﹣m的值为（ ）
A、20 B、40 C、60 D、100二、填空题
-
7. 已知△ABC≌△A'B'C'，∠A＝60°，∠B＝40°，则∠C′＝.8. 已知，如图：∠ABC＝∠DEF，AB＝DE，要说明△ABC≌△DEF，若以“ASA”为依据，还要添加的条件为.
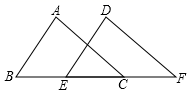
9. 若等腰三角形的两边长为3和7，则该等腰三角形的周长为.10. 如图，在Rt△ABC中，∠ACB＝90°，D是AB的中点，CD＝6 cm，则AB＝cm.
11. 如图，AD是△ABC中∠BAC的角平分线，DE⊥AB于点E，DF⊥AC于点F，S△ABC＝7，DE＝2，AB＝4，则AC长是.
12. 如图：点P为∠AOB内一点，分别作出P点关于OA、OB的对称点P1 ， P2 ， 连接P1P2交OA于M，交OB于N，P1P2=15，则△PMN的周长为 ．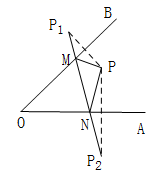
13. 如图所示，AB＝AC ， AD＝AE ， ∠BAC＝∠DAE ， ∠1＝25°，∠2＝30°，则∠3＝ ．
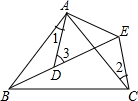14. 如图，在Rt△ABC中，∠BAC＝90°，AB＝AC，分别过点B，C作过点A的直线的垂线BD，CE，若BD＝4cm，CE＝3cm，则DE＝cm.
15. 如图，在4×4的正方形网格中，有5个小正方形已被涂黑（图中阴影部分），若在其余网格中再涂黑一个小正方形，使它与5个已被涂黑的小正方形组成的新图形是一个轴对称图形，则可涂黑的小正方形共有个.
16. 如图所示，AOB是一钢架，设∠AOB＝α，为了使钢架更加坚固，需在其内部添加一些钢管EF，FG，GH…，添加的钢管长度都与OE相等，若最多能添加这样的钢管4根，则α的取值范围是.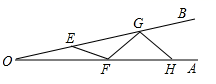
三、解答题
-
17. 如图：已知OA和OB两条公路，以及C、D两个村庄，建立一个车站P，使车站到两个村庄距离相等即PC=PD，且P到OA，OB两条公路的距离相等.
18. 如图，AB=AE，∠1=∠2，∠C=∠D．求证：△ABC≌△AED．
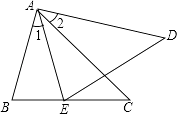19.如图，点B、E、C、F在同一条直线上，∠A=∠D，∠B=∠DEF，BE=CF．求证：AC=DF．
20. 已知：如图∠ABC＝∠ADC＝90°，M、N分别是AC、BD的中点.求证：MN⊥BD.
21. 如图，在△ABC中，AB＝AC，∠B＝30°，D为BC边上一点，∠DAB＝45°.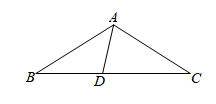
(1)、求∠DAC的度数；(2)、请说明：AB＝CD.22. 在如图网格中画图：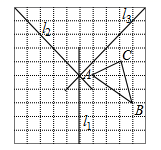
①画△A1B1C1 ， 使它与△ABC关于l1对称；
②画△A2B2C2 ， 使它与△A1B1C1关于l2对称；
③画△A3B3C3 ， 使它与△A2B2C2关于l3对称；
④画出△A3B3C3与△ABC的对称轴.
23. 如图，在△ABC中，∠C=90°，AD是∠BAC的平分线，DE⊥AB于E，F在AC上，且BD=DF.
(1)、求证：CF=EB；(2)、试判断AB与AF，EB之间存在的数量关系，并说明理由.24. 已知：如图， 和 都是等边三角形，且点A、C、E在一条直线上，AD与BE相交于点P，AD与BC相交于点M，BE与CD相交于点N.
求证：
(1)、∠APB=60°；(2)、CM=CN.25. 如图，在 中， ， ， ，
(1)、求证： .(2)、猜想： 与 之间存在怎样的数量关系？请说明理由.26. 如图，在△ABC中，∠ACB＝90°，AC＝6，BC＝8.点P从点A出发，沿折线AC—CB以每秒1个单位长度的速度向终点B运动，点Q从点B出发沿折线BC—CA以每秒3个单位长度的速度向终点A运动，P、Q两点同时出发.分别过P、Q两点作PE⊥l于E，QF⊥l于F.设点P的运动时间为t（秒）：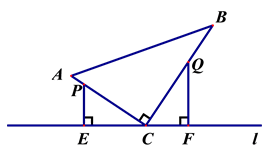
(1)、当P、Q两点相遇时，求t的值；(2)、在整个运动过程中，求CP的长（用含t的代数式表示）；(3)、当△PEC与△QFC全等时，直接写出所有满足条件的CQ的长.