江苏省泰州市医药高新区2020-2021学年八年级上学期数学第一次月考试卷
试卷更新日期：2020-10-13 类型：月考试卷
一、选择题
-
1. 下列倡导节约的图案中，是轴对称图形的是（ ）A、
B、
C、
D、
2. 下列图形具有两条对称轴的是（ ）A、等边三角形 B、平行四边形 C、矩形 D、正方形3. 如图是5×5的正方形网络，以点D，E为两个顶点作位置不同的格点三角形，使所作的格点三角形与△ABC全等，这样的格点三角形最多可以画出（ ）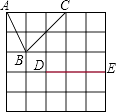
A、2个 B、4个 C、6个 D、8个4. 如图，△ABC≌△EDC，B、C、D在同一直线上，且CE=2cm，CD=3cm，则BD的长为（ ）
A、1.5cm B、2cm C、4.5cm D、6cm5. 能判定△ABC≌△A′B′C′的条件是（ ）A、AB＝A′B′，AC＝A′C′，∠C＝∠C′ B、AB＝A′B′，∠A＝∠A′，BC＝B′C′ C、AC＝A′C′，∠A＝∠A′，BC＝B′C′ D、AC＝A′C′，∠C＝∠C′，BC＝B′C′6. 如图，点C为线段AB上一点，△ACM和△CBN是等边三角形.下列结论：①AN=BM；②CE=CF；③△CEF是等边三角形；④∠ECF=60°∘.其中正确的是（ ）
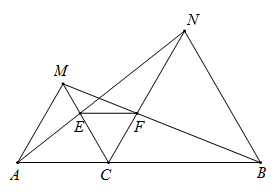A、① B、①② C、①②③ D、①②③④二、填空题
-
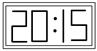
7. 在平面镜里看到背后墙上的电子钟示数如图所示，这时的实际时间应该是.
8. 如图 4×5 的方格纸中，在除阴影之外的方格中任意选择一个涂黑，与图中阴影部分构成轴对称图形的涂法有种.
9. 如图，BC=EF，AC∥DF。请你添加一个适当的条件，使得△ABC≌△DEF。（只需填一个答案即可)
10. 已知△ABC的三边长分别为5，7，8，△DEF的三边分别为5，2x，3x﹣5，若两个三角形全等，则x= ．11. 在如图所示的3×3的正方形网格中，∠1+∠2+∠3的度数为.
12. 如图，AB∥FC，E是DF的中点，若AB=30，CF=17，则BD=.
13. 如图，AB=12，CA⊥AB于A，DB⊥AB于B，且AC=4m，P点从B向A运动，每分钟走1m，Q点从B向D运动，每分钟走2m，P、Q两点同时出发，运动分钟后△CAP与△PQB全等.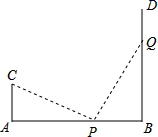
14. 如图，将△ABC折叠，使点A与BC边中点D重合，折痕为MN，若AB=9，BC=6，则△DNB的周长为.
15. 如图，在△ABC中，点D是BC上的点，∠BAD=∠ABC=40∘ ， 将△ABD沿着AD翻折得到△AED，则∠CDE=°.
16. 如图，将 沿DE折叠，使点A与BC边的中点F重合，下列结论中： ； ； ； ，正确的是 填序号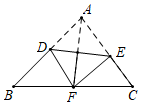
三、解答题
-
17. 如图所示，每个小正方形的边长为1，△ABC，△DEF的顶点都在小正方形的顶点处.
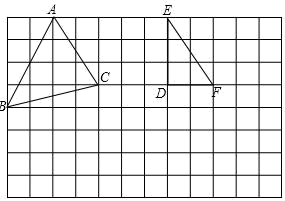
( 1 )将△ABC平移，使点A平移到点F，点B，C的对应点分别是点B′，C′，画出△FB′C′；
( 2 )画出△DEF关于DF所在直线对称的△DE′F；
( 3 )直接写出四边形B′C′FE′的面积是.
18. 在下列各图中分别补一个小正方形，使其成为不同的轴对称图形．
19. 已知：如图，AB∥ED，点F、点C在AD上，AB=DE，AF=DC.求证：BC=EF.
20. 如图，已知AC=AE，∠BAD=∠CAE，∠B=∠ADE，求证：BC=DE.
21. 如图，四边形ABCD中，AB＝AD，AC＝5，∠DAB＝∠DCB＝90°，则四边形ABCD的面积为.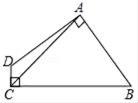
22. 如图，△ABC中，AB=AC，点E，F在边BC上，BE=CF，点D在AF的延长线上，AD=AC．
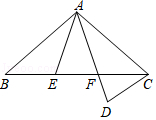(1)、求证：△ABE≌△ACF；
(2)、若∠BAE=30°，则∠ADC=°．
23. 已知：如图，点A、D、C、B在同一条直线上，AD=BC，AE=BF，CE=DF，求证：AE∥BF.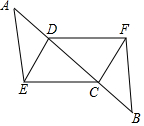
24. 如图，点A、D、C、F在同一条直线上，AD=CF，AB=DE，BC=EF.
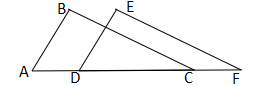(1)、求证：ΔABC≌△DEF；(2)、若∠A=55°，∠B=88°，求∠F的度数.25. 如图，点B在线段AC上，点E在线段BD上，∠ABD=∠DBC，AB=DB，EB=CB，M、N分别是AE、CD的中点．
(1)、求证：△ABE≌△DBC；(2)、判定△BMN的形状，并证明你的结论．26. 在△ABC中，AB=AC，点D是直线BC上一点(不与B. C重合)，以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE=∠BAC，连接CE.
(1)、如图1，当点D在线段BC上，如果∠BAC=90∘，则∠BCE=度；(2)、如图2，①说明：△ABD≌△ACE.
②说明：CE+DC=BC.
③设∠BAC=α，∠BCE=β.当点D在直线BC上移动，则α，β之间有怎样的数量关系?请直接写出你的结论.