四川省成都市青羊区石室教育集团2019-2020学年七年级上学期数学期中试卷

试卷更新日期：2020-10-13 类型：期中考试

进入出卷网下载

一、单选题

1. -2的倒数是（）

A、-2 B、 $- \frac{1}{2}$ C、 $\frac{1}{2}$ D、2

查看试题解析
2. 下列说法正确的是（）

A、 $\frac{1}{3}$ πx²的次数为3 B、 $\frac{1}{2}$ xy²的次数是3 C、 $\frac{2}{5}$ x﹣by³的次数是5 D、2ab+6的次数是6

查看试题解析
3. 已知a²+5a＝1，则代数式3a²+15a﹣1的值为（）

A、1 B、2 C、3 D、4

查看试题解析
4. 下列说法正确的是（）

A、所有的有理数都能用数轴上的点表示 B、符号不同的两个数互为相反数 C、有理数分为正数和负数 D、两数相加，和一定大于任何一个数

查看试题解析
5. 已知﹣2m⁶n与5m^2yn^x是同类项，则（）

A、x＝2，y＝1 B、x＝1，y＝3 C、x＝ $\frac{3}{2}$ ，y＝6 D、x＝3，y＝1

查看试题解析
6. 用一个平面去截一个正方体，截面不可能是（）

A、梯形 B、五边形 C、六边形 D、七边形

查看试题解析
7. 据报道，2019年10月7日，成都市文化广电旅游局公布的数据显示，十一黄金周期间(10月1日﹣7日)，成都市共接待游客2017.13万人次，同比增长32.7%，实现旅游收入288亿元，同比增长25.2%.288亿元用科学记数法表示正确的是（）

A、 $288 \times 10^{8}$ 元 B、 $2.88 \times 10^{10}$ 元 C、 $2.88 \times 10^{9}$ 元 D、 $2.88 \times 10^{8}$ 元

查看试题解析
8. 若m、n满足|m+3|+(n+2)²＝0，则mn的值为（）

A、﹣1 B、1 C、6 D、﹣6

查看试题解析
9. 买一支笔需要m元，买一个笔记本要n元，则买3支笔、5个笔记本共需要（）元.

A、3m+5n B、15mn C、5m+3n D、8mn

查看试题解析
10. 如图所示，一串有黑有白，其排列有一定规律的珠子，被盒子遮住一部分(如图)，则这串珠子被盒子遮住的部分(包括白色和黑色)共有（）颗.

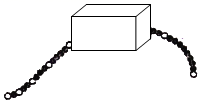A、16 B、18 C、20 D、22

查看试题解析

二、填空题

11. 一次考试中，老师采取一种记分制：得130分记为+30分，得50分记为﹣50分.那么96分应记为，李明的成绩记为﹣12分，那么他的实际得分为.

查看试题解析
12. 单项式 $\frac{4}{5}$ a²x的系数是，多项式xy﹣pqx²+ $\frac{5}{9}$ p³+9的次数是.

查看试题解析
13. 在数轴上与表示﹣1的点的距离为2的所有数是．

查看试题解析
14. 比较大小： $\frac{1}{100}$ ﹣0.009； $- \frac{2019}{2020}$ $- \frac{2020}{2019}$ .

查看试题解析
15. 如图所示，要使图中平面展开图折叠成正方体后，相对面上两个数之和为8，则x﹣y+z＝.

查看试题解析
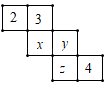16. 一个多项式加上﹣3+x﹣2x²得到x²﹣4，这个多项式是.

查看试题解析
17. 已知长方形的长是5a﹣2b，宽是2a+b，则长方形的周长为.

查看试题解析
18. 如图，已知点C在线段AB上，AC＝6，线段BC的长是线段AC长的两倍，点D是线段AB的中点，则线段CD的长是.

查看试题解析
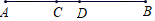19. 已知a，b为有理数，且a＞0，b＜0，a+b＜0，将四个数a，b，﹣a，﹣b按由大到小的顺序排列是．（用“＞”号连接）

查看试题解析
20. 已知|x|＝5，|y|＝3，且|x﹣y|＝y﹣x，则x﹣y＝．

查看试题解析
21. 对于有理数a，b定义一种新运算“⊙”，规定a⊙b＝|a+b|+|a﹣b|，则(﹣2)⊙(﹣3)＝.

查看试题解析
22. 已知当 $x = - 3$ 时，代数式 $a x^{3} + b x + 1$ 的值为8，那么当 $x = 3$ 时，代数式 $a x^{3} + b x + 1$ 的值为.

查看试题解析
23. 已知a、b、c在数轴上的位置如图所示，化简：|2a|﹣|a+c|﹣|b﹣1|+|﹣a﹣b|＝.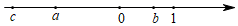

查看试题解析

三、解答题

24. 计算与合并同类项：

(1)、+4.7+(﹣4)﹣2.7﹣(﹣3.5)

(2)、11÷(﹣22)﹣3×(﹣11)

(3)、16+(﹣2)³+|﹣7|+( $- \frac{1}{8}$ )×(﹣4)

(4)、0.25×(﹣2)²﹣[﹣4÷( $- \frac{2}{3}$ )²+1]÷(﹣1)²⁰²⁰

(5)、5x⁴+3x²y﹣10﹣3x²y+x⁴﹣1

(6)、(7y﹣3z)﹣(8y﹣5z)

(7)、2(2a²+9b)+3(﹣5a²﹣6b)

(8)、﹣3(2x²﹣xy)﹣4(x²﹣xy﹣6)

查看试题解析
25. 点A，B，C，D所表示的数如图所示，回答下列问题：

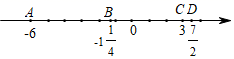(1)、A，C两点间的距离是多少？

(2)、B，D两点间的距离是多少？

查看试题解析
26. 如图，在平面内有A，B，C三点．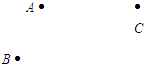

$(1)$ 画直线AC，线段BC，射线AB；

$(2)$ 在线段BC上任取一点D不同于B，C，连接线段AD；

$(3)$ 数数看，此时图中线段的条数．

查看试题解析
27. 化简并求下列代数式的值：3(a²b+ab²)﹣2(a²b﹣1)﹣2ab²﹣2，其中a＝﹣2，b＝3.

查看试题解析
28. 如图，已知线段AB和CD的公共部分为BD，且BD＝ $\frac{1}{4}$ AB＝ $\frac{1}{6}$ CD，线段AB，CD的中点E，F之间的距离是30，求线段AB，CD的长.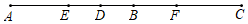

查看试题解析
29. 由8个棱长为1的相同小立方块搭成的几何体如图所示：

(1)、请画出它的三视图；

(2)、请计算它的表面积．

查看试题解析
30. 若a与b互为相反数，c与d互为负倒数，|m|＝2，求代数式 $\frac{a + b}{3}$ ﹣2cb+2m³的值.

查看试题解析
31. 已知：关于x、y的多项式 $x^{2} + a x - y + b$ 与多项式 $b x^{2} - 3 x + 6 y - 3$ 的和的值与字母x的取值无关，求代数式 $3 (a^{2} - 2 a b + b^{2}) - [4 a^{2} - 2 (\frac{1}{2} a^{2} + a b - \frac{3}{2} b^{2})]$ 的值.

查看试题解析

32. 某超市在春节期间对顾客实行优惠，规定如下：

一次性购物	优惠办法
少于200元	不予优惠
低于500元但不低于200元	九折优惠
500元或超过500元	其中500元部分给予九折优惠，超过500元部分给予八折优惠

(1)、王老师若一次性购物400元，他实际付款元.若一次性购物600元，他实际付款元.

(2)、若顾客在该超市一次性购物x元，当x小于500元但不小于200时，他实际付款元，当x大于或等于500元时，他实际付款元.(用含x的代数式表示).

(3)、如果王老师两次购物货款合计820元，第一次购物的货款为a元(200＜a＜300)，用含a的代数式表示两次购物王老师实际付款多少元？

查看试题解析