湖北省武汉黄陂区2020-2021学年八年级上学期数学开学试卷
试卷更新日期:2020-10-12 类型:开学考试
一、选择题
-
1. 若 在实数范围内有意义,则x的取值范围是( )A、 B、 C、 D、2. 如图,A,B 两点被池塘隔开,在 AB 外选一点 C,连接 AC,BC,分别取 AC,BC 的中点D,E,连接 DE.若测得 DE=5,则 AB 的长为( ).
 A、5 B、8 C、10 D、无法确定3. 如图,一木杆在离地面 3 m 处折断,木杆顶端落在离木杆底端 4 m 处,则木杆折断之前的高度为( )m.
A、5 B、8 C、10 D、无法确定3. 如图,一木杆在离地面 3 m 处折断,木杆顶端落在离木杆底端 4 m 处,则木杆折断之前的高度为( )m. A、9 B、8 C、5 D、44. 要了解某同学的数学考试成绩是否稳定,需要了解该同学近几次考试成绩的( ).A、平均数 B、中位数 C、众数 D、方差5. 一次函数 不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 如图,在 ABCD 中,对角线 AC,BD 相交于点 O,下列结论一定成立的是( )
A、9 B、8 C、5 D、44. 要了解某同学的数学考试成绩是否稳定,需要了解该同学近几次考试成绩的( ).A、平均数 B、中位数 C、众数 D、方差5. 一次函数 不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 如图,在 ABCD 中,对角线 AC,BD 相交于点 O,下列结论一定成立的是( )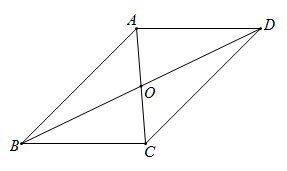 A、AC=BC B、AO=OC C、 D、7. 下图描述了某车间工人日加工零件数的情况,这些工人日加工零件数的中位数为( ).
A、AC=BC B、AO=OC C、 D、7. 下图描述了某车间工人日加工零件数的情况,这些工人日加工零件数的中位数为( ). A、4 B、5 C、6 D、78. 若点 在一次函数 的图象上,则 的大小关系是( )A、 B、 C、 D、9. 两张全等的矩形纸片 ABCD,AECF 按如图方式交叉叠放在一起,AB=AF,AE=BC.若 AB=1,BC=3,则图中重叠(阴影)部分的面积为( ).
A、4 B、5 C、6 D、78. 若点 在一次函数 的图象上,则 的大小关系是( )A、 B、 C、 D、9. 两张全等的矩形纸片 ABCD,AECF 按如图方式交叉叠放在一起,AB=AF,AE=BC.若 AB=1,BC=3,则图中重叠(阴影)部分的面积为( ). A、2 B、 C、 D、10. 如图,在平面直角坐标系中,点 ,当四边形 ABCD 的周长最小时,则 m 的值为( ).
A、2 B、 C、 D、10. 如图,在平面直角坐标系中,点 ,当四边形 ABCD 的周长最小时,则 m 的值为( ).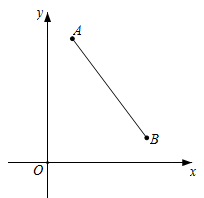 A、 B、 C、2 D、3
A、 B、 C、2 D、3二、填空题
-
11. 计算 , ,12. 某地冬季一周每日的气温记录如下,那么这周的平均气温为 ℃ ;
温度
天数
2
1
3
1
13. 将y=2x﹣3的图象向上平移2个单位长度得到的直线表达式为.14. 如图,在菱形 ABCD 中,E 为 AB 上一点,沿 CE 折叠△BEC,点 B 恰好落在对角线 AC上的 处.若∠DAB=56°,则 的度数为. 15. 甲、乙两车从 A 城出发前往 B 城.在整个行程过程中,汽车离开 A 城的距离 y 与时刻 t 的对应关系如图所示,下列结论一定正确的有 (填序号即可).①甲车行驶完全程比乙车多花 2 个小时;②乙车每小时比甲车快 40 km;③甲车与乙车在距离 B 城 150 km 处相遇;④在甲车行驶过程中共有 3 次与乙车相距 50 km.
15. 甲、乙两车从 A 城出发前往 B 城.在整个行程过程中,汽车离开 A 城的距离 y 与时刻 t 的对应关系如图所示,下列结论一定正确的有 (填序号即可).①甲车行驶完全程比乙车多花 2 个小时;②乙车每小时比甲车快 40 km;③甲车与乙车在距离 B 城 150 km 处相遇;④在甲车行驶过程中共有 3 次与乙车相距 50 km. 16. 如图,在正方形 ABCD 中,点 E 为 BC 的中点,F 为 AB 上一点,AE,CF 交于点 O.若 AB=4,∠AOF=45°,则 BF 的长为.
16. 如图,在正方形 ABCD 中,点 E 为 BC 的中点,F 为 AB 上一点,AE,CF 交于点 O.若 AB=4,∠AOF=45°,则 BF 的长为.
三、解答题
-
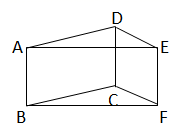
17. 计算(1)、(2)、18. 如图,四边形 ABCD 和四边形 CDEF 均为平行四边形,连接 AE,BF.求证:AE=BF.
 19. 为转变教育管理方式并为学校教育教学提供参考,某区随机抽取八年级若干名学生参加 2019 年国家义务教育质量检测,并将测试中的数学成绩 a (分数)分成 A,B,C,D,E 五个等级(A:90≤ a ≤100,B:80≤ a <90,C:70≤ a <80,D:60≤ a <70,E: a <60),绘制出了如图两幅不完整的统计图,根据以上信息,回答下列问题:
19. 为转变教育管理方式并为学校教育教学提供参考,某区随机抽取八年级若干名学生参加 2019 年国家义务教育质量检测,并将测试中的数学成绩 a (分数)分成 A,B,C,D,E 五个等级(A:90≤ a ≤100,B:80≤ a <90,C:70≤ a <80,D:60≤ a <70,E: a <60),绘制出了如图两幅不完整的统计图,根据以上信息,回答下列问题: (1)、直接写出这次质量监测数学测试抽查的学生人数;(2)、请补全条形统计图;(3)、若该区八年级共有学生 8000 人,数学成绩 a ≥80 为优秀,请估计该区八年级数学成绩达到优秀的约有多少人?20. 如图是由边长为 1 的小正方组成的网格,每个小正方形的顶点叫做格点.点 A,B 均在格点上.仅用无刻度的直尺完成画图,画图过程用虚线,画图结果用实线表示,请按步骤完成下列问题.
(1)、直接写出这次质量监测数学测试抽查的学生人数;(2)、请补全条形统计图;(3)、若该区八年级共有学生 8000 人,数学成绩 a ≥80 为优秀,请估计该区八年级数学成绩达到优秀的约有多少人?20. 如图是由边长为 1 的小正方组成的网格,每个小正方形的顶点叫做格点.点 A,B 均在格点上.仅用无刻度的直尺完成画图,画图过程用虚线,画图结果用实线表示,请按步骤完成下列问题. (1)、直接写出的 AB 长为 ;(2)、①在格点上找一点C,连接BC,使AB⊥BC;
(1)、直接写出的 AB 长为 ;(2)、①在格点上找一点C,连接BC,使AB⊥BC;②画线段AB的中点 D;
③在格点上找一点 E,连接 DE,使DE∥BC.
21. 在平面直角坐标系中,直线 向右平移1个单位长度得到直线 ;(1)、直接写出直线 的解析式;(2)、直线 分别交 x 轴, y 轴于点 A,B,交 于点 C,若 A 为 BC 的中点.①请画图并求 k 的值;
②当 时,请直接写出 x 的取值范围_▲_;
22. 随着新冠疫情防控的常态化,复工复产稳步推进,外卖订单业务量大增,某知名外卖平台招聘外卖骑手,并提供了如下两种日工资方案:方案一 :每日底薪50元,每完成一单外卖业务再提成3元;
方案二 :每日底薪80元,外卖业务的前 30 单没有提成,超过 30 单的部分,每完成一单提成 5 元.
设骑手每日完成的外卖业务量为 n(n 为正整数,单位:单),方案一、二中骑手的日工资分别为 (单位:元).
 (1)、分别写出 关于 n 的函数解析式;(2)、据统计,骑手小明外卖送单平均每天的业务量约为 50 单.若仅从日工资收入的角度考虑,他应该选择哪种日工资方案?请说明理由;(3)、某外卖骑手平均每日完成的外卖业务量为 n 单,从日工资收入的角度考虑,他应该选择哪种日工资方案?试画出日工资收入函数大致图象并直接写出你的选择方案.23. 如图,在矩形 ABCD 中,E 为 BC 上一点,以 DE 为边作矩形 DEGF,其中GF 经过点 A,连接 AE.
(1)、分别写出 关于 n 的函数解析式;(2)、据统计,骑手小明外卖送单平均每天的业务量约为 50 单.若仅从日工资收入的角度考虑,他应该选择哪种日工资方案?请说明理由;(3)、某外卖骑手平均每日完成的外卖业务量为 n 单,从日工资收入的角度考虑,他应该选择哪种日工资方案?试画出日工资收入函数大致图象并直接写出你的选择方案.23. 如图,在矩形 ABCD 中,E 为 BC 上一点,以 DE 为边作矩形 DEGF,其中GF 经过点 A,连接 AE.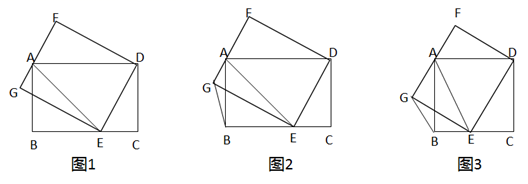 (1)、如图1,若 AE=AD,求证:AG=AF;(2)、连接BG.
(1)、如图1,若 AE=AD,求证:AG=AF;(2)、连接BG.①如图 2,若 BG=AG,CE=1,AF=2,求 AD 的长;
②如图 3,若 AB=AD,BG=BE,直接写出 的值为▲_;
24. 如图,直线 分别交 x 轴、 y 轴于A,B两点,直线 分别交 x 轴、 y 轴于 C,D,交 于点 E.
 (1)、直接写出点 A,B,D 的坐标;(2)、如图 1,若∠BED=45°,求点 C 的坐标;(3)、如图2,在(2)的条件下,过点P(m,m)作平行于x轴的直线交于M,作平行于y轴的直线交 于N,若PM≥2PN,求m的取值范围.
(1)、直接写出点 A,B,D 的坐标;(2)、如图 1,若∠BED=45°,求点 C 的坐标;(3)、如图2,在(2)的条件下,过点P(m,m)作平行于x轴的直线交于M,作平行于y轴的直线交 于N,若PM≥2PN,求m的取值范围.