贵州省遵义市桐梓县2020届九年级上学期数学期中考试试卷

试卷更新日期：2020-10-12 类型：期中考试

进入出卷网下载

一、选择题

1. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 今年1月3日，我国的嫦娥四号探测器成功在月球背面着陆，标志着我国已经成功开始了对月球背面的研究，填补了国际空白.月球距离地球的平均距离为384000千米，数据384000用科学记数法表示为（）

A、 $384 \times 10^{3}$ B、 $3.84 \times 10^{5}$ C、 $38.4 \times 10^{4}$ D、 $0.384 \times 10^{6}$

查看试题解析
3. 下列运算正确的是（）

A、 ${(a^{3})}^{2} = a^{5}$ B、 $a^{3} \times a^{2} = a^{6}$ C、 ${(a b)}^{4} = a^{4} b^{4}$ D、 $a^{6} \div a^{3} = a^{2}$

查看试题解析
4. 平面直角坐标系内一点 $P (- 2, 3)$ 关于原点对称点的坐标是（）

A、 $(3, - 2)$ B、 $(2, 3)$ C、 $(- 2, - 3)$ D、 $(2, - 3)$

查看试题解析
5. 已知a是方程x²+3x﹣1＝0的根，则代数式a²+3a+2019的值是（）

A、2020 B、﹣2020 C、2021 D、﹣2021

查看试题解析
6. 如图，AB是⊙O的直径，点C、D在⊙O上，且点C、D在AB的异侧，连接AD、BD、OD、OC，若∠ABD＝10°，且AD∥OC，则∠BOC的度数为（）

A、110° B、100° C、105° D、120°

查看试题解析
7. 已知直角三角形的两边长是方程x²﹣7x+12=0的两根，则第三边长为（）

A、7 B、5 C、 $\sqrt{7}$ D、5或 $\sqrt{7}$

查看试题解析
8. 某市2017年平均房价为每平方米5000元，2019年平均房价涨到每平方米9000元.设这两年平均房价年平均增长率为x，根据题意，下面所列方程正确的是（）

A、5000 ${(1 + x)}^{2}$ ＝9000 B、5000 ${(1 - x)}^{2}$ ＝9000 C、9000 ${(1 - x)}^{2}$ ＝5000 D、9000 ${(1 + x)}^{2}$ ＝5000

查看试题解析
9. 在同一直角坐标系中，函数 $y = m x + m$ 和函数 $y = - m x^{2} + + 2 x + 2$ （m是常数，且 $m \neq 0$ ）的图象可能是（）

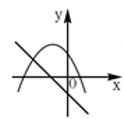A、 B、 C、 D、

查看试题解析
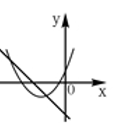10. “圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长六寸，问径几何？”用现代的数学语言表述是：“CD为 $⊙ O$ 的直径，弦 $A B ⊥ C D$ ，垂足为E，CE=1寸，AB=10寸，求直径CD的长”，依题意得CD的长为（）

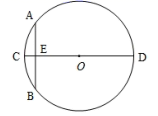A、12寸 B、13寸 C、24寸 D、26寸

查看试题解析
11. 设 $A (- 2, y_{1})$ ， $B (1, y_{2})$ ， $C (2, y_{3})$ 是抛物线 $y = - {(x + 1)}^{2} + 1$ 的三点，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系为（）

A、 $y_{1} > y_{2} > y_{3}$ B、 $y_{1} > y_{3} > y_{2}$ C、 $y_{3} > y_{2} > y_{1}$ D、 $y_{3} > y_{1} > y_{2}$

查看试题解析
12. 抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，则下列说法中：① $2 a + b = 0$ ；② $3 a + 2 b + c < 0$ ；③方程 $2 a x^{2} + 2 b x + 2 c - 5 = 0$ 没有实数根；④ $a - b > m (a m + b)$ （m为任意实数），正确的有（）个

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 若关于x的方程x²﹣2x+m＝0有一根为3，则m＝；方程另一个根为.

查看试题解析
14. 如图，在正方形ABCD中，E为DC边上的点，连接BE，将△BCE绕点C顺时针方向旋转90°，得到△DCF，连接EF，若∠BEC＝60°，BE＝4，则EF的长为.

查看试题解析
15. 如图，D，E，F分别是边BC，AD，AC上的中点，若阴影的面积为6，则△ABC的面积是.

查看试题解析
16. 如图，△ABC中，∠C＝90°，∠B＝60°，在AC边上取点O画圆，使⊙O经过A、B两点，下列结论中：①AO＝BC；②AO＝2CO；③延长BC交⊙O与D，则A、B、D是⊙O的三等分点；④以O为圆心，以OC为半径的圆与AB相切.正确的序号是.

查看试题解析

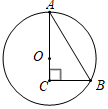
三、解答题

17. 计算： $- 1^{2019} - | \sqrt{3} - 2 | + {(\frac{1}{2})}^{- 2} + \sqrt[3]{- 8}$ .

查看试题解析
18. 用适当的方法解方程：

(1)、x²+x﹣2＝0

(2)、x(2x+3)＝4x+6.

查看试题解析
19. 为更好地践行社会主义核心价值观，让同学们珍惜粮食，学会感恩.校学生会积极倡导“光盘行动”，某天午餐后学生会干部随机调查了部分同学就餐饭菜的剩余情况，并将结果统计后绘制成如图所示的不完整的统计图.

(1)、这次被调查的同学共有名.

(2)、补全条形统计图.

(3)、计算在扇形统计图中剩一半饭菜所对应扇形圆心角的度数；

(4)、校学生会通过数据分析，估计这次被调查的所有学生一餐浪费的食物可以供40人用餐.据此估算，全校2000名学生一餐浪费的食物可供多少人食用一餐？

查看试题解析
20. 关于x的一元二次方程mx²+(2m+1)x+m＝0有两个实数根.

(1)、求m的取值范围

(2)、是否存在实数m，使方程的两实数根的倒数和为0？若存在，请求出m的值；若不存在，请说明理由.

查看试题解析
21. 某玩具商店以成本为每件60元购进一批新型玩具，以每件100元的价格销售则每天可卖出20件，为了扩大销售，增加盈利，尽快减少库存，商店决定采取适当的降价措施，经调查发现：若每件玩具每降价5元，则每天可多卖10件.

(1)、若商店平均每天盈利1200元，每件玩具的售价应定为多少元？

(2)、若商店为增加效益最大化，每件玩具的售价定为多少元时，商店平均每天盈利最多？最多盈利多少元？

查看试题解析
22. 如图，点A是⊙O直径BD延长线上的一点，AC是⊙O的切线，C为切点.AD＝CD，

(1)、求证：AC＝BC；

(2)、若⊙O的半径为1，求△ABC的面积.

查看试题解析
23. 如图，在等腰直角三角形ABC中，∠C＝90°，AB＝8 $\sqrt{2}$ ，点O是AB的中点.将一个边长足够大的Rt△DEF的直角顶点E放在点O处，并将其绕点O旋转，始终保持DE与AC边交于点G，EF与BC边交于点H.

(1)、当点G在AC边什么位置时，四边形CGOH是正方形.

(2)、等腰直角三角ABC的边被Rt△DEF覆盖部分的两条线段CG与CH的长度之和是否会发生变化，如不发生变化，请求出CG与CH之和的值：如发生变化，请说明理由.

查看试题解析
24. 抛物线y＝ax²+bx+c与x轴交于A，B两点(点A在点B的左侧)，且A(﹣1，0)，B(4，0)，与y轴交于点C，C点的坐标为(0，﹣2)，连接BC，以BC为边，点O为对称中心作菱形BDEC.点P是x轴上的一个动点，设点P的坐标为(m，0)，过点P作x轴的垂线交抛物线于点Q，交BD于点M.

(1)、求抛物线的解析式.

(2)、x轴上是否存在一点P，使三角形PBC为等腰三角形，若存在，请直接写出点P的坐标；若不存在，请说明理由.

(3)、当点P在线段OB上运动时，试探究m为何值时，四边形CQMD是平行四边形？请说明理由.

查看试题解析