贵州省遵义市赤水市2020届九年级上学期数学期中考试试卷

试卷更新日期：2020-10-12 类型：期中考试

进入出卷网下载

一、选择题

1. （-2018）⁰的值是（）

A、-2018 B、2018 C、0 D、1

查看试题解析
2. 下面四个手机应用图标中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. “五·一”期间，美丽的黄果树瀑布景区吸引大量游客前来游览.经统计，某段时间内来该风景区游览的人数约为36000人，用科学记数法表示36000为（）

A、 $3.6 \times 10^{4}$ B、 $0.36 \times 10^{6}$ C、 $0.36 \times 10^{4}$ D、 $36 \times 10^{3}$

查看试题解析
4. 如图，有一块含有30°角的直角三角形板的两个顶点放在直尺的对边上。如果∠2=44°，那么∠1的度数是（）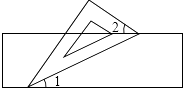

A、14° B、15° C、16° D、17°

查看试题解析
5. 下列计算正确的是（）

A、﹣a⁴b÷a²b=﹣a²b B、（a﹣b）²=a²﹣b² C、a²•a³=a⁶ D、﹣3a²+2a²=﹣a²

查看试题解析
6. 为参加全市中学生足球赛.某中学从全校学生中选拔22名足球运动员组建校足球队，这22名运动员的年龄（岁）如下表所示，该足球队队员的平均年龄是（）

年龄（岁）

12

13

14

15

人数

7

10

3

2

A、12岁 B、13岁 C、14岁 D、15岁

查看试题解析
7. 如图，蒙古包可近似看作由圆锥和圆柱组成，若用毛毡搭建一个底面圆面积为25πm² ，圆柱高为3m，圆锥高为2m的蒙古包，则需要毛毡的面积是（）

A、(30+5 $\sqrt{29}$ )πm² B、40πm² C、(30+5 $\sqrt{21}$ )πm² D、55πm²

查看试题解析
8. 已知x₁ ， x₂是关于x的方程x²+bx﹣3=0的两根，且满足x₁+x₂﹣3x₁x₂=5，那么b的值为（）

A、4 B、﹣4 C、3 D、﹣3

查看试题解析
9. 如图，在Rt△ABC中，∠ACB=90°，∠A=60°，AC=6，将△ABC绕点C按逆时针方向旋转得到△A'B'C'，此时点A'恰好在AB边上，则点B'与点B之间的距离为（）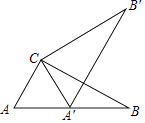

A、12 B、6 C、6 $\sqrt{2}$ D、 $6 \sqrt{3}$

查看试题解析
10. 某机械厂4月份生产零件80万个，第二季度生产零件160万个.设该厂五、六月份平均每月增长率为x，那么x满足的方程是（）

A、 $80 {(1 + x)}^{2} = 160$ B、 $80 + 80 {(1 + x)}^{2} = 160$ C、 $80 + 80 (1 + x) + 80 {(1 + x)}^{2} = 160$ D、 $80 (1 + 2 x) = 160$

查看试题解析
11. 在一个不透明的袋子里装有两个黄球和一个白球，它们除颜色外都相同，随机从中摸出一个球，记下颜色后放回袋子中，充分摇匀后，再随机摸出一个球．两次都摸到黄球的概率是（）

A、 $\frac{4}{9}$ B、 $\frac{1}{3}$ C、 $\frac{2}{9}$ D、 $\frac{1}{9}$

查看试题解析
12. 已知二次函数y＝ax²+bx+c（a≠0）的图象如图，分析下列四个结论：①abc＜0；②b²﹣4ac＞0；③3a+c＞0；④（a+c）²＜b² ，其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

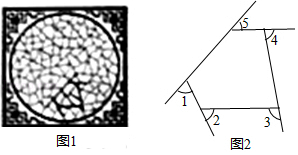
13. 计算：（3 $\sqrt{2}$ +1）（3 $\sqrt{2}$ ﹣1）= ．

查看试题解析
14. 图1是我国古代建筑中的一种窗格，其中冰裂纹图案象征着坚冰出现裂纹并开始消溶，形状无一定规则，代表一种自然和谐美.图2是从图1冰裂纹窗格图案中提取的由五条线段组成的图形，则∠1+∠2+∠3+∠4+∠5=度.

查看试题解析
15. 如图，正方形ABCD内接于⊙O，⊙O的半径为2，以点A为圆心，以AC为半径画弧交AB的延长线于点E，交AD的延长线于点F，则图中阴影部分的面积是.

查看试题解析
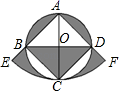16. 如图是抛物线型拱桥，当拱顶离水面2m时，水面宽4m，水面下降2m，水面宽度增加m．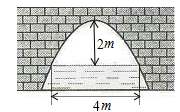

查看试题解析

三、解答题

17. 计算： $- 1^{2018} + | \sqrt{3} - 2 | + \tan 60 ° - {(π - 3.14)}^{0} + {(\frac{1}{2})}^{- 2}$ .

查看试题解析
18. 先化简，再求值： $\frac{8}{x^{2} - 4 x + 4} \div (\frac{x^{2}}{x - 2} - x - 2)$ ，其中 $| x | = 2$ .

查看试题解析
19. △ABC在平面直角坐标系中的位置如图所示.

(1)、将△ABC绕原点O顺时针旋转90°得到△A₁B₁C₁ ，请画出△A₁B₁C₁；

(2)、直接写出A₁的坐标为；

(3)、直接写出点A在旋转过程中所经过的路线长为.

查看试题解析
20. 某中学积极组织学生开展课外阅读活动，为了解本校学生每周课外阅读的时间量t（单位：小时），采用随机抽样的方法抽取部分学生进行了问卷调查，调查结果按0≤t＜2，2≤t＜3，3≤t＜4，t≥4分为四个等级，并分别用A、B、C、D表示，根据调查结果统计数据绘制成了如图所示的两幅不完整的统计图，由图中给出的信息解答下列问题：

(1)、求出x的值，并将不完整的条形统计图补充完整；

(2)、若该校共有学生2500人，试估计每周课外阅读时间量满足2≤t＜4的人数；

(3)、若本次调查活动中，九年级（1）班的两个学习小组分别有3人和2人每周阅读时间量都在4小时以上，现从这5人中任选2人参加学校组织的知识抢答赛，求选出的2人来自不同小组的概率.

查看试题解析
21. 某商店从厂家以21元的价格购进一批商品，该商品可以自行定价，若每件商品售价为a元，则可卖出（350－10a）件，但物价局限定每件商品加价不能超过进价的20%，商店计划要赚400元，需要卖出多少件商品?每件商品应售多少元？

查看试题解析
22. 阅读材料：
在平面直角坐标系xOy中，点P（x0，y0）到直线Ax+By+C=0的距离公式为： $d = \frac{| A x_{0} + B y_{0} + C |}{\sqrt{A^{2} + B^{2}}}$ .

例如：求点P0（0，0）到直线4x+3y﹣3=0的距离.

解：由直线4x+3y﹣3=0知，A=4，B=3，C=﹣3，∴点P0（0，0）到直线4x+3y﹣3=0的距离为 $d = \frac{| 4 \times 0 + 3 \times 0 - 3 |}{\sqrt{4^{2} + 3^{2}}}$ = $\frac{3}{5}$ .

根据以上材料，解决下列问题：

(1)、问题1：点P1（3，4）到直线 $y = - \frac{3}{4} x + \frac{5}{4}$ 的距离为；

(2)、问题2：已知：⊙C是以点C（2，1）为圆心，1为半径的圆，⊙C与直线 $y = - \frac{3}{4} x + b$ 相切，求实数b的值；

(3)、问题3：如图，设点P为问题2中⊙C上的任意一点，点A，B为直线3x+4y+5=0上的两点，且AB=2，请求出S△ABP的最大值和最小值.

查看试题解析
23. 如图，AB为⊙O的直径，D为 $\hat{A C}$ 的中点，连接OD交弦AC于点F，过点D作DE∥AC，交BA的延长线于点E．

(1)、求证：DE是⊙O的切线；

(2)、连接CD，若OA=AE=4，求四边形ACDE的面积．

查看试题解析
24.
如图，在平面直角坐标系中，二次函数的图象交坐标轴于A（﹣1，0），B（4，0），C（0，﹣4）三点，点P是直线BC下方抛物线上一动点．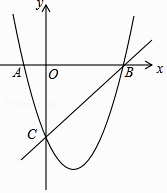

(1)、求这个二次函数的解析式；

(2)、是否存在点P，使△POC是以OC为底边的等腰三角形？若存在，求出P点坐标；若不存在，请说明理由；

(3)、动点P运动到什么位置时，△PBC面积最大，求出此时P点坐标和△PBC的最大面积．

查看试题解析

年龄（岁）	12	13	14	15
人数	7	10	3	2