甘肃省天水市2020届九年级上学期数学期中考试试卷
试卷更新日期:2020-10-12 类型:期中考试
一、选择题
-
1. 若= , 则的值为( )A、1 B、 C、 D、2. 下列式子中,属于最简二次根式的是A、 B、 C、 D、3. 下列说法中正确的是( )A、两个直角三角形相似 B、两个等腰三角形相似 C、两个等边三角形相似 D、两个锐角三角形相似4. 若方程x2+x-1=0的两实根为α、β,那么下列式子正确的是( )A、α+β=1 B、αβ=1 C、α2+β2=2 D、 + =15. 如图, ,直线a,b与 、 、 分别相交于A、B、C和D、E、F.若 , ,则EF的长是( )
 A、 B、 C、6 D、106. 某公司2016年缴税70万元,2018年缴税90万元,求该公司这两年缴税的年平均增长率. 若设该公司这两年缴税的年平均增长率为x,根据题意,可得方程( )A、70x2=90 B、70(1+x)2=90 C、70(1+x)=90 D、70+70(1+x)+70(1+x)2=907. 定义:如果一元二次方程 满足 ,那么我们称这个方程为“凤凰”方程. 已知 是“凤凰”方程,且有两个相等的实数根,则下列结论正确的是( ).A、 B、 C、 D、8. 如图,已知D,E分别是△ABC的AB,AC边上的点,DE∥BC,且S△ADE:S四边形DBCE=1:8,那么AE:AC等于( )
A、 B、 C、6 D、106. 某公司2016年缴税70万元,2018年缴税90万元,求该公司这两年缴税的年平均增长率. 若设该公司这两年缴税的年平均增长率为x,根据题意,可得方程( )A、70x2=90 B、70(1+x)2=90 C、70(1+x)=90 D、70+70(1+x)+70(1+x)2=907. 定义:如果一元二次方程 满足 ,那么我们称这个方程为“凤凰”方程. 已知 是“凤凰”方程,且有两个相等的实数根,则下列结论正确的是( ).A、 B、 C、 D、8. 如图,已知D,E分别是△ABC的AB,AC边上的点,DE∥BC,且S△ADE:S四边形DBCE=1:8,那么AE:AC等于( ) A、1:8 B、1:2 C、1:9 D、1:39. 如图所示,在矩形 中,R为 上一定点,P为 上一动点,E、F分别是 、 的中点,当点P从B向C移动时,线段 的长度( )
A、1:8 B、1:2 C、1:9 D、1:39. 如图所示,在矩形 中,R为 上一定点,P为 上一动点,E、F分别是 、 的中点,当点P从B向C移动时,线段 的长度( )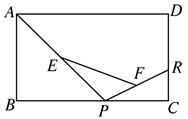 A、逐渐变小 B、逐渐变大 C、不变 D、无法确定10. 如图,一电线杆AB的影子分别落在地上和墙上,某一时刻,小明竖起1m高的直杆,量得其影长为0.5m,此时,他又量得电线杆AB落在地上的影子BD长3m,落在墙上的影子CD的高为2m,小明用这些数据很快算出了电线杆AB的高,请你计算,电线杆AB的高为( )
A、逐渐变小 B、逐渐变大 C、不变 D、无法确定10. 如图,一电线杆AB的影子分别落在地上和墙上,某一时刻,小明竖起1m高的直杆,量得其影长为0.5m,此时,他又量得电线杆AB落在地上的影子BD长3m,落在墙上的影子CD的高为2m,小明用这些数据很快算出了电线杆AB的高,请你计算,电线杆AB的高为( ) A、5m B、6m C、7m D、8m
A、5m B、6m C、7m D、8m二、填空题
-
11. 若实数a,b满足 , .12. 方程 是关于x的一元二次方程,则m=.13. 若 ,则 .14. 已知 ,则 的值为.15. 已知关于 的方程 的一个根是x=-1,则 .16. 如果一个三角形的三边长为5、12、13,与其相似的三角形的最长边的长为39,那么此三角形的周长为 , 面积为.17. 如图,已知点B、E、C、F在同一条直线上,∠A=∠D,要使△ABC∽△DEF,还需添加一个条件,你添加的条件是.(只需写一个条件,不添加辅助线和字母)
 18. 在平面直角坐标系中, 顶点A的坐标为 ,若以原点O为位似中心,画 的位似图形 ,使 与 的相似比等于 ,则点 的坐标为.
18. 在平面直角坐标系中, 顶点A的坐标为 ,若以原点O为位似中心,画 的位似图形 ,使 与 的相似比等于 ,则点 的坐标为.三、解答题
-
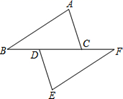
19. 计算:(1)、(2)、20. 解下列方程:(1)、(2)、(3)、21. 如图,点B、D、C、F在一条直线上,且 , ,求证: .
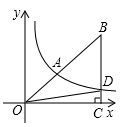
 22. 先化简,再求值: ,其中 , .23. 如图所示,双曲线 经过 斜边上的点A,且满足 ,与 交于点D, ,求k的值.
22. 先化简,再求值: ,其中 , .23. 如图所示,双曲线 经过 斜边上的点A,且满足 ,与 交于点D, ,求k的值.