甘肃省兰州市2020届九年级上学期数学期中考试试卷
试卷更新日期:2020-10-12 类型:期中考试
一、选择题
-
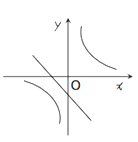
1. 顺次连接梯形各边中点所组成的图形是( )A、平行四边形 B、菱形 C、梯形 D、正方形2. 等腰三角形的一边长为4,另一边长为9,则这个三角形的周长为( )A、22 B、17 C、13 D、17或223. 已知直角三角形中30°角所对的直角边为2cm,则斜边的长为( )A、2cm B、4cm C、6cm D、8cm4. 从1到9这9个自然数中任取一个,既是2的倍数,又是3的倍数的概率是( )A、 B、 C、 D、5. 下列函数的图象,不经过原点的是( )A、 B、y=2x2 C、y=(x﹣1)2﹣1 D、6. 一个等腰梯形的两底之差为12,高为6,则等腰梯形的锐角为( )A、30° B、45° C、60° D、75°7. 下列四个点,在反比例函数y=图象上的是( )A、(1,-6) B、(2,4) C、(3,-2) D、(-6,-1)8. 关于x的函数 和 在同一坐标系中的图象大致是( ).A、
 B、
B、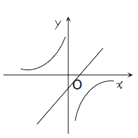 C、
C、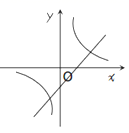 D、
D、
二、填空题
-
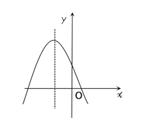
9. 若 ,则锐角α=.10. 方程(x-3)2=4的解是11. 某学校的初三(1)班,有男生20人,女生23人.现随机抽一名学生,则:抽到一名男生的概率是.12. 已知正方形ABCD的对角线长为8cm,则正方形ABCD的面积为cm2.13. 反比例函数 的图象在一、三象限,则k应满足.14. 用配方法解方程x2﹣2x﹣6=0,原方程可化为.15. 在Rt△ABC中,∠C=90°,BC=6,AB=10,sinA=.16. 菱形ABCD中,若周长是20cm,对角线AC=6cm,则对角线BD=cm.17. 关于x的一元二次方程(k-1)x2-2x+1=0有两个不相等的实数根,则实数k的取值范围是 .18. 已知二次函数 的图象如图所示,则由此可得a0,b0,c0.(填“<”或“>”)
三、解答题
-
19. 计算:20. 在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,BD:DC=2:1,BC=7.8cm,求点D到AB的距离.
 21. 如图,矩形ABCD的对角线AC、BD交于点O,∠AOD=60°,AB= ,AE⊥BD于点E,求OE的长.
21. 如图,矩形ABCD的对角线AC、BD交于点O,∠AOD=60°,AB= ,AE⊥BD于点E,求OE的长.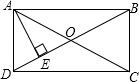 22. 在矩形ABCD中,O是对角线AC的中点,EF是线段AC的中垂线,交AD、BC于E、F.求证:四边形AECF是菱形.
22. 在矩形ABCD中,O是对角线AC的中点,EF是线段AC的中垂线,交AD、BC于E、F.求证:四边形AECF是菱形. 23. 如图,从一块长80厘米,宽60厘米的铁片中间截去一个小长方形,使截去小长方形的面积是原来铁片面积的一半,并且剩下的长方框四周的宽度一样,求这个宽度.
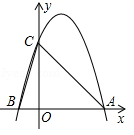
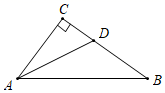
23. 如图,从一块长80厘米,宽60厘米的铁片中间截去一个小长方形,使截去小长方形的面积是原来铁片面积的一半,并且剩下的长方框四周的宽度一样,求这个宽度. 24. 如图,天空中有一个静止的广告气球C,从地面A点测得C点的仰角为45°,从地面B点测得C点的仰角为60°.已知AB=20m,点C和直线AB在同一铅垂平面上,求气球离地面的高度(结果保留根号).
24. 如图,天空中有一个静止的广告气球C,从地面A点测得C点的仰角为45°,从地面B点测得C点的仰角为60°.已知AB=20m,点C和直线AB在同一铅垂平面上,求气球离地面的高度(结果保留根号).