甘肃省定西市临洮县2020届九年级上学期数学期中考试试卷
试卷更新日期：2020-10-12 类型：期中考试
一、选择题
-
1. 下列方程，是一元二次方程的是（ ）
①3x2+x=20，②2x2-3xy+4=0，③x2- =4，④x2=0，⑤x2- +3=0
A、①② B、①④⑤ C、①③④ D、①②④⑤2. 观察下列图形，既是轴对称图形又是中心对称图形的有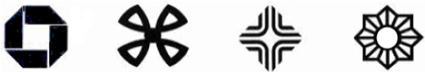
A、1个 B、2个 C、3个 D、4个3. 若 ，则x的取值范围是（ ）A、x≥7 B、x≤7 C、x＞7 D、x＜74. 过⊙O内一点M的最长弦长为10 cm ， 最短弦长为8 cm ， 那么OM为（ ）A、6 cm B、3 cm C、 cm D、9 cm5. 二次函数y=x2-2x-1的顶点在（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限6. ⊙O的半径为5cm，弦AB//CD ， 且AB=8cm，CD=6cm，则AB与CD之间的距离为( )A、1 cm B、7cm C、3 cm或4 cm D、1cm 或7cm7. 方程 与 所有根的乘积等于（ ）A、-18 B、18 C、-3 D、38.如图，在平面直角坐标系中将△ABC绕点C（0，﹣1）旋转180°得到△A1B1C1 ， 设点A1的坐标为（m，n），则点A的坐标为（ ）
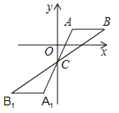A、（﹣m，﹣n） B、（﹣m，﹣n﹣2） C、（﹣m，﹣n﹣1） D、（﹣m，﹣n+1）9. 如图，在△ABC中，∠CAB=65°，将△ABC在平面内绕点A旋转到△AB′C′的位置，使CC′∥AB，则旋转角的度数为（ ）
A、30° B、40° C、50° D、65°10. 函数y=x2+bx+c与y=x的图象如图所示，有以下结论：①b2﹣4c＞0；②b+c+1=0；③3b+c+6=0；④当1＜x＜3时，x2+（b﹣1）x+c＜0．
其中正确的个数为
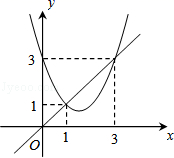A、1 B、2 C、3 D、4二、填空题
-
11. 一元二次方程 的根.12. 点A（a，3）与点B（﹣4，b）关于原点对称，则a+b＝.13. 抛物线y=2x2-4x+3绕坐标原点旋转180°所得的抛物线的解析式是.14. x2﹣10x+=（x﹣）215. 关于x的一元二次方程 有一个根为0，则m=.16. 将抛物线y=x2-2x+3向左平移一个单位，再向下平移三个单位，则抛物线的解析式应为.17. 已知方程x2-7x+12=0的两根恰好是Rt△ABC的两条边的长，则Rt△ABC的第三边长为 .18. 半径为6cm的圆中，垂直平分半径OA的弦长为cm.
三、解答题
-
19. 某企业2015年收入2500万元，2017年收入3600万元.(1)、求2015年至2017年该企业收入的年平均增长率；(2)、根据(1)所得的平均增长率，预计2018年该企业收入多少万元？20. 在等腰△ABC中，三边分别为a，b，c，其中a=5，若关于x的方程x2+（b﹣2）x+b﹣3=0有两个相等的实数根，求△ABC的周长.21. 解方程：（x2+x）2+（x2+x）＝6.22. 在实数范围内定义运算“⊕”，其法则为：a⊕b＝a2﹣b2 ， 求方程（4⊕3）⊕x＝24的解.23. 某商场销售一批名牌衬衫，平均每天可销售20件，每件赢利40元.为了扩大销售，增加赢利，商场决定采取适当降价措施.经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出2件.(1)、若该商场平均每天要赢利1200元，且让顾客尽可能得到实惠，每件衬衫应降价多少元?(2)、求该商场平均每天赢利的最大值。24. 如图，⊙O的直径为10，圆心O到弦AB的距离OM的长为3，则弦AB的长是 ．
25. 如图，将半径为2cm的圆形纸片折叠后，圆弧恰好经过圆心O，求折痕AB的长.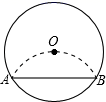
26. 在平面直角坐标系中，O 为原点，点 A（4，0），点 B（0，3），把△ABO 绕点 B 逆时针旋转，得△A′BO′，点 A、O 旋转后的对应点为 A′、O′，记旋转角为ɑ.
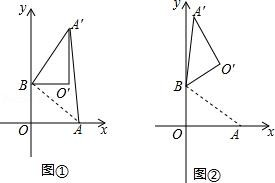(1)、如图 1，若ɑ＝90°，求 AA′的长；(2)、如图 2，若ɑ＝120°，求点 O′的坐标.27. 如图，利用一面长 的墙，用 长的篱笆，围成一个长方形的养鸡场.
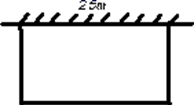(1)、怎样围成一个面积为 的长方形养鸡场？(2)、能否围成一个面积为 的长方形养鸡场？如能，说明围法；如不能，请说明理由.28. 如图，已知二次函数y=ax2+2x+c的图象经过点C（0，3），与x轴分别交于点A，点B（3，0）．点P是直线BC上方的抛物线上一动点．
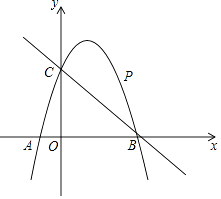(1)、求二次函数y=ax2+2x+c的表达式；(2)、连接PO，PC，并把△POC沿y轴翻折，得到四边形POP′C．若四边形POP′C为菱形，请求出此时点P的坐标；(3)、当点P运动到什么位置时，四边形ACPB的面积最大？求出此时P点的坐标和四边形ACPB的最大面积．