云南省临沧市镇康县2020届九年级上学期数学期中考试试卷

试卷更新日期：2020-10-12 类型：期中考试

进入出卷网下载

一、填空题

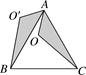
1. 一元二次方程 $2 x^{2} - 2 = 0$ 的解是．

查看试题解析
2. 如果关于x的二次函数 $y = x^{2} - 2 x + k$ 与x轴只有1个交点，则 $k =$ .

查看试题解析
3. 如图，△ABC为等边三角形，△AO′B绕点A逆时针旋转后能与△AOC重合，则∠OAO′＝度．

查看试题解析
4. 设m ， n是一元二次方程x²＋2x－7＝0的两个根，则m²＋3m＋n＝.

查看试题解析
5. 已知关于x的一元二次方程 $x^{2} + (2 k + 1) x + k^{2} - 2 = 0$ 的两根x₁和x₂ ，且 $(x_{1} - 2) (x_{1} - x_{2}) = 0$ ，则k的值是.

查看试题解析
6. 廊桥是我国古老的文化遗产 $.$ 如图，是某座抛物线型的廊桥示意图，已知抛物线的函数表达式为 $y = - \frac{1}{40} x^{2} + 10$ ，为保护廊桥的安全，在该抛物线上距水面AB高为8米的点E，F处要安装两盏警示灯，则这两盏灯的水平距离EF是米 $. ($ 精确到1米 $)$

查看试题解析

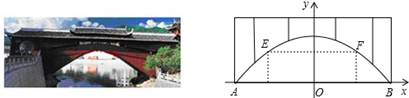
二、选择题

7. 二次函数y=x²﹣2x+2的顶点坐标是（）

A、（1，1） B、（2，2） C、（1，2） D、（1，3）

查看试题解析
8. 下列图形中，是轴对称图形，但不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
9. 若x＝－2是关于x的一元二次方程x²＋ $\frac{3}{2}$ ax－a²＝0的一个根，则a的值为（）

A、－1或4 B、－1或－4 C、1或－4 D、1或4

查看试题解析
10. 设x₁ ， x₂是一元二次方程x²﹣2x﹣5＝0的两根，则x₁²+x₂²的值为（）

A、6 B、8 C、14 D、16

查看试题解析
11. 若一次函数y=ax+b（a≠0）的图象与x轴的交点坐标为（﹣2，0），则抛物线y=ax²+bx的对称轴为（）

A、直线x=1 B、直线x=﹣2 C、直线x=﹣1 D、直线x=﹣4

查看试题解析
12. 已知抛物线y＝ax²＋bx＋c(a<0)过A(－3，0)，B(1，0)，C(－5，y₁)，D(5，y₂)四点，则y₁与y₂的大小关系是（）

A、y₁>y₂ B、y₁＝y₂ C、y₁<y₂ D、不能确定

查看试题解析
13. 关于x的一元二次方程(m－2)x²＋(2m＋1)x＋m－2＝0有两个不相等的正实数根，则m的取值范围是(　　)

A、m＞ $\frac{3}{4}$ B、m＞ $\frac{3}{4}$ 且m≠2 C、－ $\frac{1}{2}$ ≤m≤2 D、 $\frac{3}{4}$ ＜m＜2

查看试题解析
14. 如图，抛物线y＝ax²＋bx＋c(a≠0)的对称轴为直线x＝1，与x轴的一个交点坐标为(－1，0)，其部分图象如图所示，下列结论：①4ac＜b²；②方程ax²＋bx＋c＝0的两个根是x₁＝－1，x₂＝3；③3a＋c＞0；④当y＞0时，x的取值范围是－1≤x＜3；⑤当x＜0时，y随x增大而增大．其中结论正确的个数是（）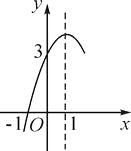

A、4个 B、3个 C、2个 D、1个

查看试题解析

三、解答一

15. 解方程：x²-2x-8=0．

查看试题解析
16. 已知关于x的一元二次方程x²-kx-2=0,求证：无论k为何值，方程总有两个不相等的实数根.

查看试题解析
17. 如图，在边长为1的小正方形组成的方格纸上，将△ABC绕着点A顺时针旋转90°

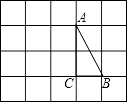(1)、画出旋转之后的△AB′C′；

(2)、求线段AC旋转过程中扫过的扇形的面积．

查看试题解析
18. 已知抛物线y＝ax²－2ax＋c与x轴交于A，B两点，与y轴正半轴交于点C，且A(－1，0)．

(1)、一元二次方程ax²－2ax＋c＝0的解是；

(2)、一元二次不等式ax²－2ax＋c＞0的解集是；

(3)、若抛物线的顶点在直线y＝2x上，求此抛物线的解析式．

查看试题解析
19. 已知关于x的一元二次方程x²－(2k＋1)x＋4k－3=0，当Rt△ABC的斜边a= $\sqrt{31}$ ，且两直角边b和c恰好是这个方程的两个根时，求△ABC的周长.

查看试题解析
20. 2016年3月国际风筝节在铜仁市万山区举办，王大伯决定销售一批风筝，经市场调研：蝙蝠形风筝进价每个为10元，当售价为每个12元时，销售量为180个，若售价每提高1元，销售量就会减少10个，请解答以下问题：

(1)、用表达式表示蝙蝠形风筝销售量y(个)与售价x(元)之间的函数关系(12≤x≤30)；

(2)、王大伯为了让利给顾客，并同时获得840元利润，售价应定为多少？

(3)、当售价定为多少时，王大伯获得利润最大，最大利润是多少？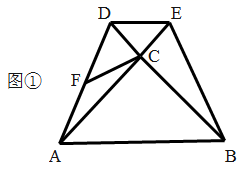

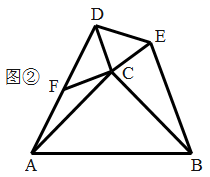查看试题解析
21. 如图，在 $Δ A B C$ 和 $Δ C D E$ 中， $A C = B C$ ， $C D = C E$ ， $∠ A C B + ∠ D C E = 180 °$ ， $Δ A B C$ 不动， $Δ C D E$ 绕点C旋转，连接 $A D$ ， $B E$ ，F为 $A D$ 的中点，连接 $C F$ .

(1)、如图①，当 $∠ A C D = 90 °$ 时，求证： $B E = 2 C F$ ；

(2)、当 $∠ A C D \neq 90 °$ 时，（1）的结论是否成立；请结合图②说明理由.

查看试题解析
22. 如图，已知△ABC是等边三角形，以AB为直径作⊙O，交BC边于点D，交AC边于点F，作DE⊥AC于点E．

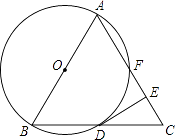(1)、求证：DE是⊙O的切线；

(2)、若△ABC的边长为4，求EF的长度．

查看试题解析
23. 如图，在平面直角坐标系中，已知抛物线经过A(－4，0)，B(0，－4)，C(2，0)三点．

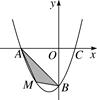(1)、求抛物线的解析式；

(2)、若点M为第三象限内抛物线上一动点，点M的横坐标为m ， △AMB的面积为S ，求S关于m的函数关系式，并求出S的最大值；

(3)、若点P是抛物线上的动点，点Q是直线y＝－x上的动点，判断有几个位置能使以点P ， Q ， B ， O为顶点的四边形为平行四边形(要求PQ∥OB)，直接写出相应的点Q的坐标．

查看试题解析