江苏省江阴市四校2019-2020学年高二上学期数学期中考试试卷

试卷更新日期：2020-10-10 类型：期中考试

进入出卷网下载

一、单选题

1. 不等式x²-5x+6＜0的解集是（）

A、 ${x | x > 1$ 或 $x < - 6}$ B、 ${x | x > 6$ 或 $x < - 1}$ C、 ${x | x > 3$ 或 $x < 2}$ D、 ${x | 2 < x < 3}$

查看试题解析
2. $\sqrt{3} - 1$ 与 $\sqrt{3} + 1$ 的等比中项是（）

A、 $\sqrt{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\pm \sqrt{2}$ D、 $\pm \frac{\sqrt{2}}{2}$

查看试题解析
3. 已知椭圆 $\frac{x^{2}}{m - 2} + \frac{y^{2}}{10 - m} = 1$ 的长轴在x轴上，焦距为4，则m的值为（）

A、8 B、4 C、8或4 D、以上答案都不对

查看试题解析
4. “ $a = - 2$ ”是“直线 $l_{1} : a x - y + 3 = 0 与 l_{2} : 2 x - (a + 1) y + 4 = 0$ 互相平行”的（）

A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
5. 已知数列{a_n}是递增的等比数列，a₄=4a₂ ， a₁+a₅=17，则S₂₀₁₉-2a₂₀₁₉的值为（）

A、1 B、-1 C、 $1 - 2^{2020}$ D、 $1 - 2^{2019}$

查看试题解析
6. 若椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ （其中a＞b＞0）的离心率为 $\frac{3}{5}$ ，两焦点分别为F₁ ， F₂ ， M为椭圆上一点，且△F₁F₂M的周长为16，则椭圆C的方程为（）

A、 $\frac{x^{2}}{16} + \frac{y^{2}}{25} = 1$ B、 $\frac{x^{2}}{25} + \frac{y^{2}}{9} = 1$ C、 $\frac{x^{2}}{9} + \frac{y^{2}}{25} = 1$ D、 $\frac{x^{2}}{25} + \frac{y^{2}}{16} = 1$

查看试题解析
7. 若正数a、b满足ab=a+b+3，则ab的取值范围是（）

A、 $[9, + \infty)$ B、 $(- \infty, 1] \cup [9, + \infty)$ C、 $(0, 1] \cup [9, + \infty)$ D、 $[1, 9]$

查看试题解析
8. 《张丘建算经》有一道题大意为：今有十等人，每等一人，宫赐金，依等次差(即等差)降之，上三人先入，得金四斤，持出，下四人后入得金三斤，持出，中间三人未到者，亦依等次更给，则每等人比下一等人多得（）斤？

A、 $\frac{5}{81}$ B、 $\frac{7}{78}$ C、 $\frac{4}{39}$ D、 $\frac{7}{76}$

查看试题解析
9. 若关于x的不等式x²-mx+4＞0在x∈[1，3]上有解，则实数m的取值范围为（）

A、 $(- \infty, 5)$ B、 $(- \infty, 5]$ C、 $(- \infty, 4)$ D、 $(- \infty, - 4) \cup (4, + \infty)$

查看试题解析
10. 某公司租地建仓库，每月土地占用费y₁与仓库到车站的距离成反比，而每月库存货物的运费y₂与到车站的距离成正比，如果在距离车站10km处建仓库，这两项费用y₁和y₂分别为2万元和8万元，那么要使这两项费用之和最小，仓库应建在距离车站（）

A、4km B、5km C、6km D、7km

查看试题解析
11. 设f（n）=2+2³+2⁵+2⁷+…+2²ⁿ⁺⁷（n∈Z），则f（n）等于（）

A、 $\frac{2}{3} (4^{n} - 1)$ B、 $\frac{2}{3} (4^{n + 1} - 1)$ C、 $\frac{2}{3} (4^{n + 3} - 1)$ D、 $\frac{2}{3} (4^{n + 4} - 1)$

查看试题解析
12. 已知等差数列{a_n}首项为a，公差为1， $b_{n} = \frac{a_{n} + 1}{a_{n}}$ ，若对任意的正整数n都有b_n≥b₅ ，则实数a的取值范围是（）

A、 $(- \infty, - 4) \cup (- 3, + \infty)$ B、 $(- 4, - 3)$ C、 $(- \infty, - 5) \cup (- 4, + \infty)$ D、 $(- 5, - 4)$

查看试题解析

二、填空题

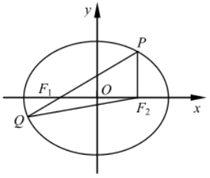
13. 命题“∀x∈R，x²+2x+2＞0”的否定为．

查看试题解析
14. 在等比数列{a_n}中，a_n＞a_n+1且a₇•a₁₁=6，a₄+a₁₄=5，则 $\frac{a_{6}}{a_{16}}$ = ．

查看试题解析
15. 已知椭圆的方程为 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ （a＞b＞0），过椭圆右焦点且与x轴垂直的直线与椭圆交于P，Q两点，直线 $x = \frac{a^{2}}{c}$ 与x轴交于点M，若△PQM为正三角形，则椭圆的离心率为．

查看试题解析
16. 已知x＞0，y＞0，且 $\frac{1}{x} + \frac{1}{y} = 1$ ，则 $\frac{9 x}{1 - x} + \frac{4 y}{1 - y}$ 的最大值为．

查看试题解析

三、解答题

17. 已知关于x的不等式：ax²-2（a+1）x+4＞0，a∈R．

(1)、当a=-4时，求不等式的解集；

(2)、当a＞0时，求不等式的解集．

查看试题解析
18. 在等差数列{a_n}中，a₂=3，a₅=6．

(1)、求数列{a_n}的通项公式；

(2)、设 $b_{n} = \frac{1}{a_{n} a_{n + 1}}$ ，求数列{b_n}的前n项和S_n ．

查看试题解析
19. 已知函数f（x）=x²+ax+3．

(1)、当x∈R时，f（x）≥a恒成立，求a的取值范围．

(2)、当a∈[4，6]时，f（x）≥0恒成立，求x的取值范围．

查看试题解析
20. 某地区现有一个直角梯形水产养殖区ABCD，∠ABC=90°，AB∥CD，AB=800m，BC=1600m，CD=4000m，在点P处有一灯塔（如图），且点P到BC，CD的距离都是1200m，现拟将养殖区ACD分成两块，经过灯塔P增加一道分隔网EF，在△AEF内试验养殖一种新的水产品，当△AEF的面积最小时，对原有水产品养殖的影响最小．设AE=d．

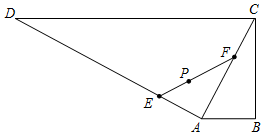(1)、若P是EF的中点，求d的值；

(2)、求对原有水产品养殖的影响最小时的d的值，并求△AEF面积的最小值．

查看试题解析
21. 在数列{a_n}中，已知 $a_{1} = \frac{3}{2}$ ，且2a_n+1=a_n+1（n∈N^*）．

(1)、求证：数列{a_n-1}是等比数列；

(2)、若b_n=na_n ，求数列{b_n}的前n项和T_n ．

查看试题解析
22. 如图，在平面直角坐标系xOy中，椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ （a＞b＞0）的左、右焦点分别为F₁ ， F₂ ， P为椭圆C上一点，且PF₂垂直于x轴，连结PF₁并延长交椭圆于另一点Q，设 $| \overset{⇀}{P Q} |$ =λ $| \overset{⇀}{F_{1} Q} |$ ．

(1)、若点P的坐标为（2，3），求椭圆C的方程及λ的值；

(2)、若4≤λ≤5，求椭圆C的离心率的取值范围．

查看试题解析