四川省自贡市富顺县富顺三中、代寺学区2019-2020学年八年级上学期数学期中试卷
试卷更新日期：2020-10-10 类型：期中考试
一、单选题
-
1. 已知三角形三边长分别为2，9， ，若 为偶数，则这样的三角形个数为（ ）A、1个 B、2个 C、3个 D、4个2. 若一个正n边形的每个内角为144°，则n等于( )A、10 B、8 C、7 D、53. 已知等腰三角形的周长为17cm，一边长为4cm，则它的腰长为（ ）A、4cm B、6.5cm或9cm C、6.5cm D、4cm或6.5cm4. 如图，将一副三角板如图放置，若AE∥BC ， 则∠BAD＝（ ）
A、90° B、85° C、75° D、65°5. 等腰 中， ，用尺规作图作出线段BD，则下列结论错误的是（ ）
A、 B、 C、 D、 的周长6. 如图，在△ABC中，∠C＝90°，∠A＝30°，AB的垂直平分线分别交AB，AC于点D，E，则下列结论正确的是（ ）
A、AE＝3CE B、AE＝2CE C、AE＝BD D、BC＝2CE7. 如图，将纸片△ABC沿着DE折叠，若∠1+∠2=60°，则∠A的大小为（ ）
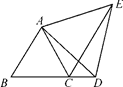
A、20° B、25° C、30° D、35°8. 下列说法正确的是（ ）A、等腰三角形的高、中线、角平分线互相重合 B、等腰三角形的两个底角相等 C、顶角相等的两个等腰三角形全等 D、等腰三角形一边不可以是另一边的2倍9. 如图，在△ABC 中，∠B=90º，AC=10，AD 为此三角形的一条角平分线，若 BD=3，则三角形 ADC 的面积为（ ）
A、3 B、10 C、12 D、1510. 如图，△ABC≌△AED ， 点E在线段BC上，∠1＝40°，则∠AED的度数是（ ）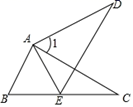
A、70° B、68° C、65° D、60°11. 如果点P（-2，b）和点Q（a，-3）关于x轴对称，则 的值是（ ）A、1 B、-1 C、5 D、-512. 如图，一个正五边形和一个正方形都有一边在直线l上，且有一个公共顶点B ， 则∠ABC的度数是（ ）
A、120° B、142° C、144° D、150°二、填空题
-
13. 线段、角、三角形、圆中，其中轴对称图形有 个．14. 等腰三角形一腰上的高与另一腰的夹角为38°，则该等腰三角形的底角的度数为15. 如图，在△ABC中，∠C＝90°，∠B＝15°，DE垂直平分AB ， 垂足是点E ， 若BD＝8cm ． 则AC的长是。
16. 如图，在△ABC中，点D是∠ABC和∠ACB的角平分线的交点，∠A＝80°，∠ABD＝30°，则∠DCB为。
17. 如图，直线m是△ABC中BC边的垂直平分线，点P是直线m上的一动点．若AB＝6，AC＝4，BC＝7，则△APC周长的最小值是。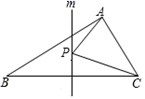
18. 如图，已知∠MON＝30°，点A1 ， A2 ， A3 ， …在射线ON上，点B1 ， B2 ， B3 ， …在射线OM上，△A1B1A2 ， △A2B2A3 ， △A3B3A4 ， …均为等边三角形，若OA1＝1，则△A8B8A9的边长。
三、解答题
-
19.
如图，在直角△ABC中，∠C＝90°，∠CAB的平分线AD交BC于D，若DE垂直平分AB，求∠B的度数．
20. 如图，在△AOB中，点C在OA上，点E，D在OB上，且CD∥AB，CE∥AD，AB＝AD，求证：△CDE是等腰三角形．
21. 如图，BD是等边三角形ABC的角平分线，E是BC延长线上的一点，且CE=CD，DF=BC，垂足为F．BF与EF相等吗？为什么？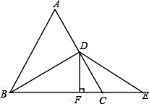
22. 叙述并证明线段垂直平分线的性质。23. 如图，点D在AB上，点E在AC上，BE、CD相交于点O.
(1)、若∠A=50°，∠BOD=70°，∠C=30°，求∠B的度数；(2)、试猜想∠BOC与∠A+∠B+∠C之间的关系，并证明你猜想的符合题意性.24. 如图，在四边形ABCD中，BC＞BA，AD=DC，
(1)、若BD⊥CD，∠C=60°，BC=10，求AD的长；(2)、若BD平分∠ABC，求证：∠A+∠C=180°．
