四川省南充市嘉陵区多校联考2019-2020学年八年级上学期数学期中试卷
试卷更新日期：2020-10-10 类型：期中考试
一、单选题
-
1. 在生活中，我们要把安全时时刻刻记在心间，图中的图形是常见的安全标记，其中是轴对称图形的是（ ）A、
B、
C、
D、
2. 一个多边形的内角和是外角和的2倍，这个多边形是（ ）
A、四边形 B、五边形 C、六边形 D、八边形3. 如图，△ABC和△DEF中，AB=DE、角∠B=∠DEF，添加下列哪一个条件无法证明△ABC≌△DEF（ ）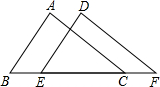
A、AC∥DF B、∠A=∠D C、AC=DF D、∠ACB=∠F4. 如图，一个等边三角形纸片，剪去一个角后得到一个四边形，则图中∠α+∠β的度数是（ ）
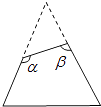A、180° B、220° C、240° D、300°5. 如图，△ABC与 关于直线l对称，则 B的度数为（ ）
A、80° B、90° C、100° D、110°6. 如图，把一块含有30°角（∠A=30°）的直角三角板ABC的直角顶点放在矩形桌面CDEF的一个顶点C处，桌面的另一个顶点F与三角板斜边相交于点F，如果∠1=40°，那么∠AFE=（ ）
A、50° B、40° C、20° D、10°7. 如图，△ABC≌△ADE，若∠E=70°，∠D=30°，∠CAD=35°，则∠BAD的度数为（ ）
A、40° B、45° C、50° D、55°8. 如图，AD是△ABC的角平分线，DE⊥AB于E ， △ABC的面积为10，AB＝6，DE＝2，则AC的长是（ ）．
A、4 B、4.5 C、4.8 D、59. 下列命题中，正确的是（ ）A、三角形的一个外角大于任何一个内角 B、三角形的一条中线将三角形分成两个面积相等的三角形 C、两边和其中一边的对角分别相等的两个三角形全等 D、三角形的三条高都在三角形内部10. 如图，△ABC中，以B为圆心，BC长为半径画弧，分别交AC，AB于D，E，连接BD，DE，若∠A=30°，AB=AC，则∠BDE的度数为（ ）．
A、52.5° B、60° C、67.5° D、75°二、填空题
-
11. 一个等腰三角形的两边长分别为5或6，则这个等腰三角形的周长是
．
12. 已知三角形的两边长分别为5和7，则第三边 的取值范围是.13. 已知点 和 关于x轴对称，则 的值为 ．14.如图，在△ABC中，AC=BC，△ABC的外角∠ACE=100°，则∠A= 度．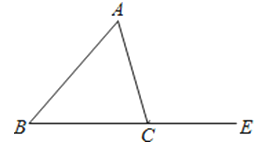
15. 如图，在Rt△ABC中， B=90 ，ED是AC的垂直平分线，交AC于点D，交BC于点E．若 BAE=50 ，则 = ．
16. 如图，在等腰△ABC中，AB＝AC，∠BAC＝50°．∠BAC的平分线与AB的中垂线交于点O，点C沿EF折叠后与点O重合，则∠CEF的度数是 ．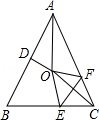
三、解答题
-
17. 已知一个十边形中，九个内角的和的度数是1290 ，求这个十边形的另一个角的度数．18. 如图，在Rt△ABC和Rt△BAD中，AB为斜边，AC=BD ， BC ， AD相交于点E ．
求证：∠ABC=∠BAD ．
19. 如图，五边形ABCDE的内角都相等，EF平分∠AED ． 求证：EF⊥BC ．
20.如图，点C，E，F，B在同一直线上，点A，D在BC异侧，AB∥CD，AE=DF，∠A=∠D．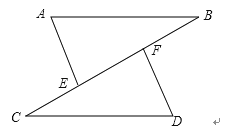
(1)、求证：AB=CD．(2)、若AB=CF，∠B=30°，求∠D的度数．21. 把下面的图形补充成关于直线l对称的图形．（不写画法，保留痕迹）
22. 如图，网格中有格点△ABC与△DEF．
(1)、△ABC与△DEF是否全等？（不说理由．）(2)、△ABC与△DEF是否成轴对称？（不说理由．）(3)、若△ABC与△DEF成轴对称，请画出它的对称轴l．并在直线l上画出点P，使PA+PC最小．
