四川省广元市苍溪县2019-2020学年八年级上学期数学期中试卷
试卷更新日期：2020-10-10 类型：期中考试
一、单选题
-
1. 下列各组字母（大写）都是轴对称图形的是（ ）．A、A、D、E B、F、E、C C、P、R、W D、H、K、L2. 若等腰三角形的一边长等于5，另一边长等于3，则它的周长等于（ ）．A、10 B、11 C、13 D、11或133. 三角形的下列线段中，能将三角形的面积分成相等两部分的是( )A、中线 B、角平分线 C、高 D、中位线4. 一个正多边形的的每个内角为120°，则这个正多边形的边数是（ ）．A、5 B、6 C、7 D、85. 如果一个等腰三角形的一个内角等于40°，则该等腰三角形的底角的度数为（ ）．A、40° B、70° C、40°或70° D、都不是6. 小芳有两根长度为4cm和9cm的木条，她想钉一个三角形木框，桌上有下列长度的几根木条，她应该选择长度为（ ）的木条．A、5cm B、3 cm C、17cm D、12 cm7. 如图，AD是∠BAC的平分线，DE⊥AB于点E， ，DE=2，AB=4，则AC的长是（ ）．
A、5 B、6 C、8 D、78. 已知：如图，在△ABC中，AB=AC，DE是AB的垂直平分线，若BE+CE=12，BC=8，则△ABC的周长为（ ）
A、20 B、32 C、24 D、369. 如图，AE=AF，AB=AC，EC与BF交于点O，∠A=60°，∠B=25°，则∠EOB的度数为（ ）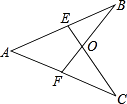
A、60° B、70° C、75° D、85°10. 如图，在 中， ，D是AB上的点，过点D作 交BC于点F ， 交AC的延长线于点E ， 连接CD ， ，则下列结论正确的有（ ）
①∠DCB=∠B；②CD= AB；③△ADC是等边三角形；④若∠E=30°，则DE=EF+CF ．
A、①②③ B、①②④ C、②③④ D、①②③④二、填空题
-
11. 已知点A（a+1,－2)与点B(－1,1-b)关于x轴对称,则a +b= .12. 如果一个三角形的三条高的交点恰好是三角形的一个顶点，那么这个三角形是 ．13. 若等腰三角形的底角等于15°，腰长为4cm，则等腰三角形的面积为.14. 一个多边形的内角和是其外角和的2倍，则这个多边形的对角线是条.15. 已知三角形的三边长分别为2，a－1，4，则化简|a－3|－|a－7|的结果为 ．
三、解答题
-
16. 作图题：（不写作法，但必须保留作图痕迹）(1)、如图，已知点M.N和∠AOB，求作一点P，使P到点M.N的距离相等，且到∠AOB的两边的距离相等．
(2)、要在河边修建一个水泵站，分别向张村.李庄送水（如图）． 修在河边l什么地方，可使所用水管最短？试在图中确定水泵站的位置．
17. 如图，在△ABC中，直线l交AB于点M，交BC于点N，点B关于直线l的对称点D在线段BC上，且AD⊥MD，∠B=28°，求∠DAB的度数．
18. 如图，在△ABC中，∠A=30°，∠B=60°，CF平分∠ACB．
(1)、求∠ACE的度数．(2)、若CD⊥AB于点D，∠CDF=75°，求证：△CFD是直角三角形．19. 如图，Rt△ABC的直角顶点C置于直线l上，AC＝BC，现过A．B两点分别作直线l的垂线，垂足分别为点D．E．
(1)、求证：△ACD≌△CBE．(2)、若BE＝3，DE＝5，求AD的长．20. 如图：已知在△ABC中，AB=AC，D为BC边的中点，过点D作DE⊥AB，DF⊥AC，垂足分别为E，F．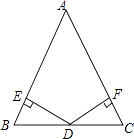
(1)、求证：DE=DF；(2)、若∠A=60°，BE=1，求△ABC的周长．21. 如图，DE⊥AB于E ， DF⊥AC于F ， 若BD＝CD ， BE＝CF ．
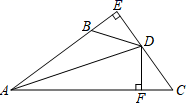(1)、求证：AD平分∠BAC ．(2)、写出AB+AC与AE之间的等量关系，并说明理由．
