四川省成都市简阳市镇金学区2019-2020学年八年级上学期数学期中试卷

试卷更新日期：2020-10-10 类型：期中考试

进入出卷网下载

一、单选题

1. 在 $\frac{22}{7}$ ， $\sqrt{8}$ ，–3.1416，π， $\sqrt{25}$ ，0.161161116……， $\sqrt[3]{9}$ 中无理数有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
2. 下列说法：①－ $\sqrt{17}$ 是17的平方根；② $\frac{1}{27}$ 的立方根是± $\frac{1}{3}$ ；③－81没有立方根④实数和数轴上的点一一对应。其中错误的有（）

A、①③ B、①④ C、②③ D、②④

查看试题解析
3. 实数 $- \sqrt{7}, - 2.5, - 3$ 的大小关系是（）

A、 $- \sqrt{7} < - 2.5 < - 3$ B、 $- 3 < - \sqrt{7} < - 2.5$ C、 $- 2.5 < - \sqrt{7} < - 3$ D、 $- 3 < - 2.5 < - \sqrt{7}$

查看试题解析
4. 已知一个直角三角形的两边长分别为3和4，则第三边长是（）

A、5 B、25 C、 $\sqrt{7}$ D、5或 $\sqrt{7}$

查看试题解析
5. 在坐标平面内有一点P（x，y），若xy=0，那么点P的位置在（ )

A、原点 B、x轴上 C、y轴上 D、坐标轴上

查看试题解析
6. 下面四组数中是勾股数的一组是（）

A、6,7,8； B、5,8,13； C、3,2,2.5; D、5，12，13

查看试题解析
7. 如果直线AB平行于y轴，则点A，B的坐标之间的关系是（）

A、横坐标相等 B、纵坐标相等 C、横坐标的绝对值相等 D、纵坐标的绝对值相等

查看试题解析
8. 在平面直角坐标系中，点P（﹣1，1）关于x轴的对称点在（　　）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
9. 已知点M到x轴的距离为3，到y轴的距离为2，则M点的坐标为（）

A、(3，2) B、(－3，－2) C、(3，－2) D、(2，3)，(2，－3)，(－2，3)，(－2，－3)

查看试题解析
10. 点M（1，2）关于x轴对称的点的坐标为（）

A、（1，﹣2） B、（2，﹣1） C、（﹣1，﹣2） D、（﹣1，2）

查看试题解析

二、填空题

11. $\sqrt{16}$ 的算术平方根是， $\sqrt{5}$ ﹣2的相反数是　， $\sqrt[3]{- 8}$ 的绝对值是．

查看试题解析
12. 已知实数x、y满足|y﹣ $\sqrt{3}$ |+ $\sqrt{x - 2}$ =0，则y^x= ．

查看试题解析
13. 已知点 $A (a - 1, a + 1)$ 在x轴上，则a等于.

查看试题解析
14. 大于 $- \sqrt{5}$ 且小于 $\sqrt{3}$ 的所有整数的和是。

查看试题解析
15. 一个实数的两个平方根分别是a+3和2a－5，则这个实数是.

查看试题解析
16. 已知－2<x<1，则 $\sqrt{x^{2} + 4 x + 4} + \sqrt{x^{2} - 2 x + 1}$ 化简的结果是.

查看试题解析
17. 已知，等腰三角形ABC的周长为16cm，底边BC上的高AD长为4cm，则三角形ABC的面积；

查看试题解析
18. 已知：如图，在Rt ∆ABC中， $∠ C = 90^{°}$ ，AB=5cm， AC=3cm，动点P从点B出发沿射线BC以2cm/s 的速度移动，设运动的时间为t秒.t= 时三角形ABP为直角三角形.

查看试题解析
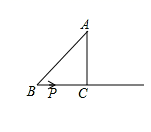19. 三角形ABC中，AB=5， $A C = 4 \sqrt{2}$ ，BC边上的高AD=4，BC=

查看试题解析

三、解答题

20. 计算

(1)、 $5 \sqrt{2} - \sqrt{8} - 7 \sqrt{18}$

(2)、 $\sqrt{24} - \sqrt{\frac{1}{3}} - 4 \sqrt{\frac{1}{8}}$

(3)、（ $3 \sqrt{12} - 2 \sqrt{\frac{1}{3}} + \sqrt{48}) \div 2 \sqrt{3}$

查看试题解析
21. 如图，从高8米的电杆AC的顶部A处，向地面的固定点B处拉一根铁丝，若B点距电杆底部的距离为6米.现在准备一根长为9.9米长的铁丝，够用吗？请你说明理由.

查看试题解析
22. 已知等边 $△ A B C$ 的两个顶点的坐标为 $A (- 4 ， 0)$ ， $B (2 ， 0)$ ，试求 $C$ 点的坐标和 $△ A B C$ 的面积．

查看试题解析
23. 如图，正方形ABCD以 $(0 ， 0)$ 为中心，边长为4，求各顶点的坐标．

查看试题解析
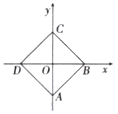24. 已知 $\sqrt{1 - 3 a}$ 和︱8b－3︱互为相反数，求 ${(a b)}^{- 2}$ －27 的值.

查看试题解析
25. 已知关于x的一次函数y=mx+4m﹣2．

(1)、若这个函数的图象经过原点，求m的值；

(2)、若这个函数的图象不过第四象限，求m的取值范围；

(3)、不论m取何实数这个函数的图象都过定点，试求这个定点的坐标．

查看试题解析
26. 阅读下列题目的解题过程：
已知a、b、c为△ABC的三边，且满足a²c²﹣b²c²=a⁴﹣b⁴ ，试判断△ABC的形状．

解：∵a²c²﹣b²c²=a⁴﹣b⁴ （A）

∴c²（a²﹣b²）=（a²+b²）（a²﹣b²）（B）

∴c²=a²+b² （C）

∴△ABC是直角三角形

问：

(1)、上述解题过程，从哪一步开始出现不符合题意？请写出该步的代号：；

(2)、错误的原因为：；

(3)、本题正确的结论为：．

查看试题解析
27. 阅读下列材料，然后回答问题：
在进行类似于二次根式 $\frac{2}{\sqrt{3} + 1}$ 的运算时，通常有如下两种方法将其进一步化简：

方法一： $\frac{2}{\sqrt{3} + 1} = \frac{2 (\sqrt{3} - 1)}{(\sqrt{3} + 1) (\sqrt{3} - 1)} = \frac{2 (\sqrt{3} - 1)}{{(\sqrt{3})}^{2} - 1^{2}} = \sqrt{3} - 1$

方法二： $\frac{2}{\sqrt{3} + 1} = \frac{{(\sqrt{3})}^{2} - 1^{2}}{\sqrt{3} + 1} = \frac{(\sqrt{3} + 1) (\sqrt{3} - 1)}{\sqrt{3} + 1} = \sqrt{3} - 1$

(1)、请用两种不同的方法化简： $\frac{2}{\sqrt{5} + \sqrt{3}}$ ；

(2)、化简： $\frac{2}{\sqrt{4} + \sqrt{2}} + \frac{2}{\sqrt{6} + \sqrt{4}} + \frac{2}{\sqrt{8} + \sqrt{6}} + \cdot \cdot \cdot + \frac{2}{\sqrt{2012} + \sqrt{2010}}$ .

查看试题解析
28. 如图，已知一次函数 $y = - \frac{1}{2} x + 3$ 的图象与x轴、y轴分别交于点A，B．

(1)、求点A，B的坐标；

(2)、M为ー次函数y=x+3的图象上一点，若 △ABM与△ABO的面积相等，求点M的坐标；

(3)、Q为y轴上的一点，若三角形ABQ为等腰三角形，请直接写出点Q的坐标.

查看试题解析