四川省成都市大邑县2019-2020学年八年级上学期数学期中试卷
试卷更新日期:2020-10-10 类型:期中考试
一、单选题
-
1. 下列实数中,无理数是A、 B、 C、 D、2. 下列各式正确的是( )A、 B、 C、 D、3. 五根小木棒,其长度分别为7,15,20,24,25,现将它们摆成两个直角三角形,如图,其中正确的是( )A、
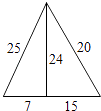 B、
B、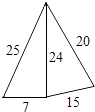 C、
C、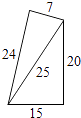 D、
D、 4. 如图,点A(﹣2,1)到y轴的距离为( )
4. 如图,点A(﹣2,1)到y轴的距离为( ) A、﹣2 B、1 C、2 D、5. 如图,直角三角形三边向外作正方形,字母A所代表的正方形的面积为( )
A、﹣2 B、1 C、2 D、5. 如图,直角三角形三边向外作正方形,字母A所代表的正方形的面积为( ) A、4 B、8 C、16 D、646. 如图,以数轴的单位长线段为边作一个正方形,以数轴的原点为旋转中心,将过原点的对角线顺时针旋转,使对角线的另一端点落在数轴正半轴的点A处,则点A表示的数是
A、4 B、8 C、16 D、646. 如图,以数轴的单位长线段为边作一个正方形,以数轴的原点为旋转中心,将过原点的对角线顺时针旋转,使对角线的另一端点落在数轴正半轴的点A处,则点A表示的数是 A、 B、1.4 C、 D、7. 要使二次根式 有意义,那么x的取值范围是( )A、x>2 B、x<2 C、x≥2 D、x≤28. 在平面直角坐标系中,点A(5,-2)关于y轴对称点的坐标为( )A、(﹣5,﹣2) B、(5,2) C、(﹣5,2) D、(﹣2,5)9. 一次函数 的图像正确的是( )A、
A、 B、1.4 C、 D、7. 要使二次根式 有意义,那么x的取值范围是( )A、x>2 B、x<2 C、x≥2 D、x≤28. 在平面直角坐标系中,点A(5,-2)关于y轴对称点的坐标为( )A、(﹣5,﹣2) B、(5,2) C、(﹣5,2) D、(﹣2,5)9. 一次函数 的图像正确的是( )A、 B、
B、 C、
C、 D、
D、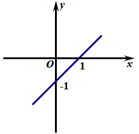 10. 已知点 和 都在直线 上,则 的大小关系是( )A、 B、 C、 D、大小不确定
10. 已知点 和 都在直线 上,则 的大小关系是( )A、 B、 C、 D、大小不确定二、填空题
-
11. 比较大小: (填 , ,或 ).12. 已知点 在第四象限内,且到 轴的距离是 ,到 轴的距离是 ,则点 的坐标是 .13. 如图所示,一次函数y=ax+b的图象与x轴相交于点(2,0),与y轴相交于点(0,4),结合图象可知,关于x的方程ax+b=0的解是 .
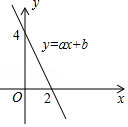 14. 如右图,一只蚂蚁沿着边长为2的正方体表面从点A出发,经过3个面爬到点B,如果它运动的路径是最短的,则此最短路径的长为.
14. 如右图,一只蚂蚁沿着边长为2的正方体表面从点A出发,经过3个面爬到点B,如果它运动的路径是最短的,则此最短路径的长为.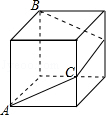 15. 已知 ,则 的值是 .16. 已知实数 为△ABC的两边,且满足 ,第三边 则第三边c上的高的值是 .17. 如图,由四个全等的直角三角形拼成的大正方形的面积为84,中间小正方形的面积为24,若直角三角形较长直角边为 ,较短直角边为 ,则 .
15. 已知 ,则 的值是 .16. 已知实数 为△ABC的两边,且满足 ,第三边 则第三边c上的高的值是 .17. 如图,由四个全等的直角三角形拼成的大正方形的面积为84,中间小正方形的面积为24,若直角三角形较长直角边为 ,较短直角边为 ,则 . 18. 如图,长方形ABCD中,AB=2,BC=4,点E是BC边上一点,连接AE , 把∠B沿AE折叠,使点B落在点B′处.当△CEB′为直角三角形时,BE的长为 .
18. 如图,长方形ABCD中,AB=2,BC=4,点E是BC边上一点,连接AE , 把∠B沿AE折叠,使点B落在点B′处.当△CEB′为直角三角形时,BE的长为 . 19. 如图,正方形A1B1C1O,A2B2C2C1 , A3B3C3C2…按如图所示放置,点A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,则A4的坐标是 , 通过你对A1、A2、A3…坐标的研究发现,得出An的坐标是 .
19. 如图,正方形A1B1C1O,A2B2C2C1 , A3B3C3C2…按如图所示放置,点A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,则A4的坐标是 , 通过你对A1、A2、A3…坐标的研究发现,得出An的坐标是 .
三、解答题
-
20. 计算:(1)、(2)、21. 计算:(1)、(2)、22. 《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”翻译成数学问题是:如图所示,在 中, ,求 的长.
 23. 已知 的平方根是 , 的立方根是3, 是 的算术平方根.(1)、填空:a=、b=、 = .(2)、若 的整数部分是 ,小数部分是y,求 的值24. 如图,直线 与x轴相交于点A,与y轴相交于点B.
23. 已知 的平方根是 , 的立方根是3, 是 的算术平方根.(1)、填空:a=、b=、 = .(2)、若 的整数部分是 ,小数部分是y,求 的值24. 如图,直线 与x轴相交于点A,与y轴相交于点B. (1)、求A、B两点的坐标;(2)、过B点作直线BP与x轴相交于P,且使AP=2OA, 求ΔBOP的周长.25. 如图,把长方形纸片OABC放入直角坐标系中,使OA, OC分别落在x轴、y轴的正半轴上,连接AC,将 翻折,点B落在该坐标平面内,设这个落点为D,CD交x轴于点E,已知CB=8,AB=4.
(1)、求A、B两点的坐标;(2)、过B点作直线BP与x轴相交于P,且使AP=2OA, 求ΔBOP的周长.25. 如图,把长方形纸片OABC放入直角坐标系中,使OA, OC分别落在x轴、y轴的正半轴上,连接AC,将 翻折,点B落在该坐标平面内,设这个落点为D,CD交x轴于点E,已知CB=8,AB=4. (1)、求AC所在直线的函数关系式;(2)、求点E的坐标和 的面积:(3)、求点D的坐标,并判断点(8,-4)是否在直线OD上,说明理由.26. 如图,某沿海城市A接到台风警报,在该市正南方向 千米有一台风中心正在B处形成,并沿着北偏东45°的BC方向以15千米/小时的速度向C移动,AD⊥BC于D,如果在距台风中心150千米的区域内都将受到台风的影响,请问:
(1)、求AC所在直线的函数关系式;(2)、求点E的坐标和 的面积:(3)、求点D的坐标,并判断点(8,-4)是否在直线OD上,说明理由.26. 如图,某沿海城市A接到台风警报,在该市正南方向 千米有一台风中心正在B处形成,并沿着北偏东45°的BC方向以15千米/小时的速度向C移动,AD⊥BC于D,如果在距台风中心150千米的区域内都将受到台风的影响,请问: (1)、通过计算说明,台风会否影响到A市?(2)、画图计算说明,台风中心从B处出发后,经过几小时会影响到A市,对A市持续影响的时间有多少小时?在第几小时时对A市的影响最大?27. 观察下列等式:
(1)、通过计算说明,台风会否影响到A市?(2)、画图计算说明,台风中心从B处出发后,经过几小时会影响到A市,对A市持续影响的时间有多少小时?在第几小时时对A市的影响最大?27. 观察下列等式:① ;
② ;
③ ;…
回答下列问题:
(1)、化简: =; =;(n为正整数);(2)、利用上面所揭示的规律计算:+…+ + .
(3)、若 , . 求 的值.28. 如图1,在平面直角坐标系中,点A坐标为(−4,4),点B的坐标为(2,0). (1)、求线段AB的长;(2)、点M是坐标轴上的一个点,若以AB为直角边构造直角三角形△ABM,请求出满足条件的所有点M的坐标;(3)、如图2,以点A为直角顶点作∠CAD=90°,射线AC交x轴的负半轴与点C,射线AD交y轴的负半轴与点D,当∠CAD绕点A旋转时,OC−OD的值是否发生变化?若不变,直接写出它的值;若变化,直接写出它的变化范围(不要求写解题过程).
(1)、求线段AB的长;(2)、点M是坐标轴上的一个点,若以AB为直角边构造直角三角形△ABM,请求出满足条件的所有点M的坐标;(3)、如图2,以点A为直角顶点作∠CAD=90°,射线AC交x轴的负半轴与点C,射线AD交y轴的负半轴与点D,当∠CAD绕点A旋转时,OC−OD的值是否发生变化?若不变,直接写出它的值;若变化,直接写出它的变化范围(不要求写解题过程).