湖南省株洲市株洲县2019-2020学年八年级上学期数学期中试卷
试卷更新日期:2020-10-10 类型:期中考试
一、单选题
-
1. 若分式 有意义,则x的取值范围是( )A、x>5 B、x≠5 C、x=5 D、x<52. 将分式 中的 , 的值同时扩大为原来的2019倍,则变化后分式的值( )A、扩大为原来的2019倍 B、缩小为原来的 C、保持不变 D、以上都不符合题意3. 下列运算正确的是( )A、 B、 C、 D、4. 下列长度的3根小木棒不能搭成三角形的是( )A、2cm,3cm,4cm B、1cm,2cm,3cm C、3cm,4cm,5cm D、4cm,5cm,6cm5. 将一副直角三角板按如图所示的位置放置,使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边放在同一条直线上,则∠α的度数是( )。
 A、45° B、60° C、75° D、85°6. 若一个三角形三个内角的度数之比为1:2:3,则这个三角形是( )A、锐角三角形 B、等边三角形 C、钝角三角形 D、直角三角形7. 世界文化遗产“三孔”景区已经完成5G基站布设,“孔夫子家”自此有了5G 网络.5G网络峰值速率为4G 网络峰值速率的10倍,在峰值速率下传输500兆数据,5G 网络比4G 网络快45秒,求这两种网络的峰值速率.设4G网络的峰值速率为每秒传输 兆数据,依题意,可列方程是( )A、 B、 C、 D、8. 如图,在△ABC中,BD平分∠ABC , ED//BC , 已知AB=3, AD=1,则△AED的周长为( )
A、45° B、60° C、75° D、85°6. 若一个三角形三个内角的度数之比为1:2:3,则这个三角形是( )A、锐角三角形 B、等边三角形 C、钝角三角形 D、直角三角形7. 世界文化遗产“三孔”景区已经完成5G基站布设,“孔夫子家”自此有了5G 网络.5G网络峰值速率为4G 网络峰值速率的10倍,在峰值速率下传输500兆数据,5G 网络比4G 网络快45秒,求这两种网络的峰值速率.设4G网络的峰值速率为每秒传输 兆数据,依题意,可列方程是( )A、 B、 C、 D、8. 如图,在△ABC中,BD平分∠ABC , ED//BC , 已知AB=3, AD=1,则△AED的周长为( ) A、2 B、3 C、4 D、59. 如图, 是 的边 的垂直平分线,D为垂足, 交 于点E,且 ,则 的周长是( )
A、2 B、3 C、4 D、59. 如图, 是 的边 的垂直平分线,D为垂足, 交 于点E,且 ,则 的周长是( )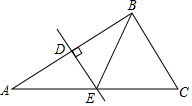 A、12 B、13 C、14 D、1510. 如果等边三角形一边上的高为 ,那么其周长是( )A、 B、 C、 D、
A、12 B、13 C、14 D、1510. 如果等边三角形一边上的高为 ,那么其周长是( )A、 B、 C、 D、二、填空题
-
11. 计算: = .12. 当x=1时,分式 的值是 .13. 已知方程 ,如果设 ,那么原方程可以变形成关于 的方程为 .14. 关于x的方程 有增根,则k的值是.15. 命题“三角形的三个内角中至少有两个锐角”是(填“真命题”或“假命题”).16. 如图,已知在 和 中, , ,点 、 、 、 在同一条直线上,若使 ,则还需添加的一个条件是(只填一个即可).
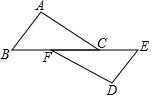 17. 如图,直线 , 的顶点 在直线 上,边 与直线 相交于点 .若 是等边三角形, ,则 =°
17. 如图,直线 , 的顶点 在直线 上,边 与直线 相交于点 .若 是等边三角形, ,则 =°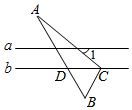 18. 若 , , ,…;则a2011的值为 . (用含m的代数式表示)
18. 若 , , ,…;则a2011的值为 . (用含m的代数式表示)三、解答题
-
19. 计算.(1)、(2)、20. 解关于 的分式方程.(1)、(2)、 ;21. 化简式子( 1) ,并在﹣2,﹣1,0,1,2中选取一个合适的数作为a的值代入求值.22. 为提高学生的阅读兴趣,某学校建立了共享书架,并购买了一批书籍.其中购买A种图书花费了3000元,购买B种图书花费了1600元,A种图书的单价是B种图书的1.5倍,购买A种图书的数量比B种图书多20本.(1)、求A和B两种图书的单价;(2)、书店在“世界读书日”进行打折促销活动,所有图书都按8折销售学校当天购买了A种图书20本和B种图书25本,共花费多少元?23. 如图,在△ABC中,点D、E分别在边AC、AB上,BD=CE,∠DBC=∠ECB.

求证:AB=AC.
24. 如图,点 , 在 上, , , ,求证: .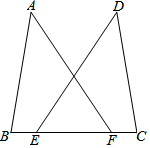 25. 已知: .
25. 已知: .求作: ,使得 .
作法:
①以 为圆心,任意长为半径画弧,分别交 , 于点 ;
②画一条射线 ,以点 为圆心, 长为半径画弧,交 于点 ;
③以点 为圆心, 长为半径画弧,与第②步中所画的弧相交于点 ;
④过点 画射线 ,则 .

根据上面的作法,完成以下问题:
(1)、使用直尺和圆规,作出 (请保留作图痕迹).(2)、完成下面证明 的过程(注:括号里填写推理的依据).证明:由作法可知 , , ,
∴ ≌ ()
∴ .()
26. 在等腰 和等腰 中, , ,连接 交于点 .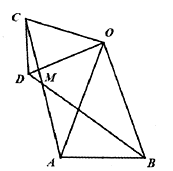 图1
图1 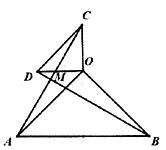
图2
(1)、如图1,若 :① 与 的数量关系为;
② 的度数为;
(2)、如图2,若 :①判断 与 之间存在怎样的数量关系?并说明理由;
②求 的度数;